Advertisements
Advertisements
Question
Prove that any four vertices of a regular pentagon are concylic (lie on the same circle).
Solution

ABCDE is a regular pentagon.
∴ `∠BAE = ∠ABC = ∠BCD = ∠CDE = ∠DEA = ((5 - 2)/5) xx 180^circ = 180^circ`
In ΔAED,
AE = ED ...(Sides of regular pentagon ABCDE)
∴ ∠EAD = ∠EDA
In ΔAED,
∠AED + ∠EAD + ∠EDA = 180°
`=>` 108° + ∠EAD + ∠EAD = 180°
`=>` 2∠EAD = 180° − 108° = 72°
`=>` ∠EAD = 36°
∴ ∠EDA = 36°
∠BAD = ∠BAE − ∠EAD = 108° − 36° = 72°
In quadrilateral ABCD,
∠BAD + ∠BCD = 108° + 72° = 180°
∴ ABCD is a cyclic quadrilateral
APPEARS IN
RELATED QUESTIONS
PQRS is a cyclic quadrilateral. Given ∠QPS = 73°, ∠PQS = 55° and ∠PSR = 82°, calculate:
1) ∠QRS
2) ∠RQS
3) ∠PRQ

The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic. Prove it.
If two non-parallel sides of a trapezium are equal, it is cyclic. Prove it. Or An isosceles trapezium is always cyclic. Prove it.
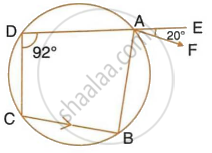
In the given figure, ABCD is a cyclic quadrilateral. AF is drawn parallel to CB and DA is produced to point E. If ∠ADC = 92°, ∠FAE = 20°; determine ∠BCD. Give reason in support of your answer.
In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°.

Find:
- ∠CAD
- ∠CBD
- ∠ADC
In following figure , O is the centre of the circle. If ∠ APB = 50° then find ∠ AOB and ∠ OAB.

In the given figure, AB is the diameter. The tangent at C meets AB produced at Q.

If ∠ CAB = 34° , find : ∠ CQB
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BEC
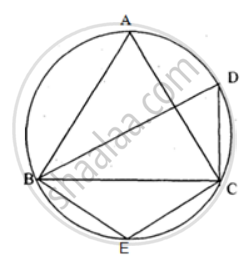
Prove that the angle bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (Provided they are not parallel) intersect at the right angle.
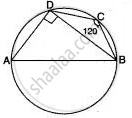
In the adjoining figure, AB is the diameter of the circle with centre O. If ∠BCD = 120°, calculate:
(i) ∠BAD (ii) ∠DBA