Advertisements
Advertisements
प्रश्न
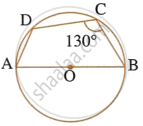
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130o. Find:
1) ∠DAB
2) ∠DBA

उत्तर
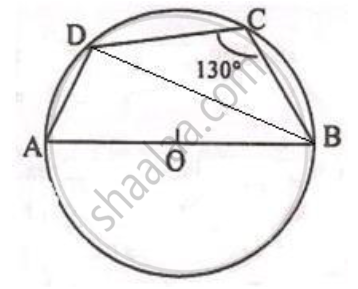
Given: AB is the diameter of the circle with centre O, ∠BCD = 130°
To find: ∠DAB, ∠DBA
1) Clearly, ABCD is a cyclic quadrilateral.
We know, the sum of a pair of opposite angles of a cyclic quadrilateral is 180°
∴ ∠DAB + ∠DCB = 180°
⇒ ∠DAB + 130° = 180°
⇒ ∠DAB = 180° - 130° = 50°
2) Consider ΔDAB,
Here, ∠ADB = 90° …..[Since angle in a semi-circle is a right angle]
So, by angle sum property of a triangle,
∠DAB + ∠DBA + ∠ADB = 180°
⇒ 50° + ∠DBA + 90° = 180°
⇒ ∠DBA = 180° - 140° = 40°
APPEARS IN
संबंधित प्रश्न
In the given figure, AB = AC. Prove that DECB is an isosceles trapezium.
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If ∠BCG = 108° and O is the centre of the circle, find :
- angle BCT
- angle DOC

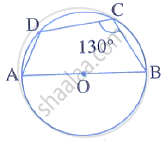
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130°. Find:
(i) ∠DAB
(ii) ∠DBA
In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65° , find the remaining angles.
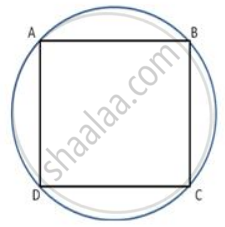
In a cyclic quadrialteral ABCD , if m ∠ A = 3 (m ∠C). Find m ∠ A.
ABCD is a parallelogram. A circle through vertices A and B meets side BC at point P and side AD at point Q. Show that quadrilateral PCDQ is cyclic.
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BDC
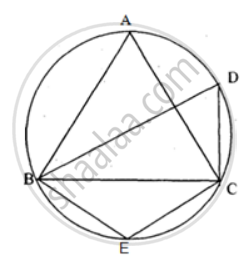
If ABCD is a cyclic quadrilateral in which AD || BC. Prove that ∠B = ∠C.
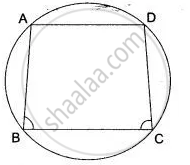
The diagonals of a cyclic quadrilateral are at right angles. Prove that the perpendicular from the point of their intersection on any side when produced backward bisects the opposite side.
In the given figure, AB is the diameter of a circle with centre O.
∠BCD = 130°. Find:
- ∠DAB
- ∠DBA