Advertisements
Advertisements
प्रश्न
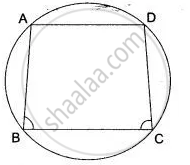
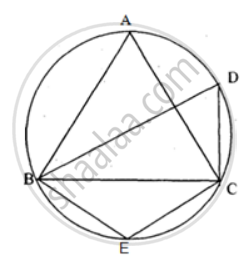
If ABCD is a cyclic quadrilateral in which AD || BC. Prove that ∠B = ∠C.
उत्तर
ABCD is a cyclic quadrilateral.
So, ∠A + ∠C = 180° ...(i)
Since AD || BC
So, ∠B + ∠A = 180° ....(ii)
From (i) and (ii)
∠A + ∠C = ∠B + ∠A
∠C = ∠B
or ∠B = ∠C
Hence proved.
APPEARS IN
संबंधित प्रश्न
PQRS is a cyclic quadrilateral. Given ∠QPS = 73°, ∠PQS = 55° and ∠PSR = 82°, calculate:
1) ∠QRS
2) ∠RQS
3) ∠PRQ

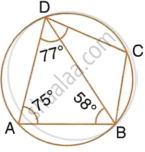
In the figure, given below, ABCD is a cyclic quadrilateral in which ∠BAD = 75°; ∠ABD = 58° and ∠ADC = 77°. Find:
- ∠BDC,
- ∠BCD,
- ∠BCA.
ABCD is a cyclic quadrilateral in which BC is parallel to AD, angle ADC = 110° and angle BAC = 50°. Find angle DAC and angle DCA.
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic. Prove it.
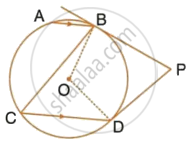
In the given figure, O is the centre of the circle. The tangents at B and D intersect each other at point P. If AB is parallel to CD and ∠ABC = 55°, find:
- ∠BOD
- ∠BPD
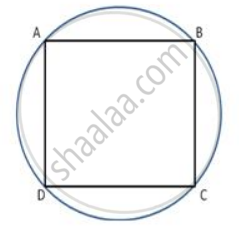
In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65 ° , find the remaining angles
In the given figure, AB is the diameter. The tangent at C meets AB produced at Q.

If ∠ CAB = 34° , find : ∠ CQB
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BDC
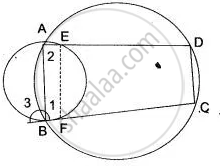
In Fig. ABCD is a cyclic quadrilateral. A circle passing through A and B meets AD and BC in the points E and F respectively. Prove that EF || DC.
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

