Advertisements
Advertisements
प्रश्न
Two equal circles intersect in P and Q. A straight line through P meets the circles in A and B. Prove that QA = QB
उत्तर
Let C (O, r) and C(O', r) be two equal circles. clearly, C(O, r) ≅ C(O', r).
Since PQ is a common chord of two congruent circles.
Therefore,
arc PCQ = arc PDQ
⇒ ∠ QAP = ∠ QBP
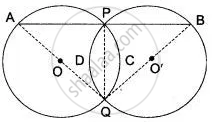
Thus, in ΔQAB, we have
∠ QAP = ∠ QBP
⇒ QA = QB
Hence proved.
APPEARS IN
संबंधित प्रश्न
A straight line is drawn cutting two equal circles and passing through the mid-point M of the line joining their centres O and O’
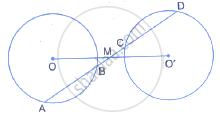
Prove that the chords AB and CD, which are intercepted by the two circles are equal.
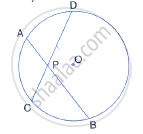
Two equal chords AB and CD of a circle with centre O, intersect each other at point P inside the circle, prove that:
(i) AP = CP,
(ii) BP = DP
OABC is a rhombus whose three vertices A, B and C lie on a circle with centre O. If the radius of the circle is 10 cm, find the area of the rhombus.
In a circle, with centre O, a cyclic quadrilateral ABCD is drawn with AB as a diameter of the circle and CD equal to radius of the circle. If AD and BC produced meet at point P; show that ∠APB = 60°.
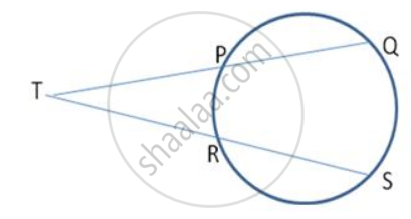
In fig. the centre of the circle is O. PQ and RS are two equal chords of the circle which , when produced , meet at T outside the circle . Prove that (a) TP = TR (b) TQ = TS.
Two congruent drdes have their centres at 0 and P. Mis the midpoint of the line segment OP. A straight line is drawn through M cutting the two circles at the points A, B, C and D. Prove that the chords AB and CD are equal.
In the given Figure, AB and CD are two chords of a circle, intersecting each other at P such that AP = CP. Show that AB= CD.
Two equal chords AB and CD of a circle with center O, intersect each other at point P inside the circle.
Prove that: (i) AP = CP ; (ii) BP = DP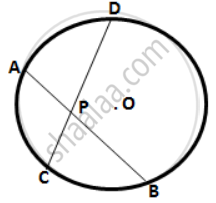
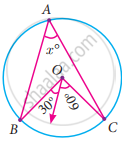
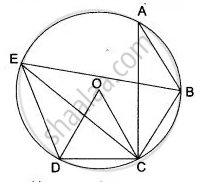
In the adjoining diagram, chords AB, BC and CD are equal. O is the centre of the circle. If ∠ ABC = 120°, Calculate: (i) ∠ BAC, (ii) ∠ BEC, (iii) ∠ BED, (iv) ∠ COD
Find the value of x° in the following figure: