Advertisements
Advertisements
प्रश्न
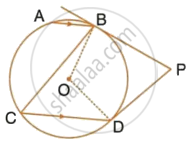
In the given figure, O is the centre of the circle. The tangents at B and D intersect each other at point P. If AB is parallel to CD and ∠ABC = 55°, find:
- ∠BOD
- ∠BPD
उत्तर
In the given figure, O is the centre of the circle AB || CD, ∠ABC = 55° tangents at B and D are drawn which meet at P.
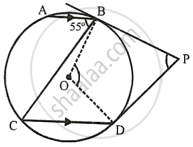
∵ AB || CD
∴ ∠ABC = ∠BCD ...(Alternate angles)
∴ ∠ABC = 55° ...(Given)
i. Now arc BD subtands ∠BOD at the centre and ∠BCD at the remaining part of the circle.
∴ ∠BOD = 2∠BCD
= 2 × 55°
= 110°
ii. In quadrilateral OBPD,
∠OBP = ∠ODP = 90° ...(∵ BP and DP are tangents)
∴ ∠BOD + ∠BPD = 180°
`\implies` 110° + ∠BPD = 180°
`\implies` ∠BPD = 180° – 110° = 70°
Hence, ∠BOD = 110° and ∠BPD = 70°
APPEARS IN
संबंधित प्रश्न
PQRS is a cyclic quadrilateral. Given ∠QPS = 73°, ∠PQS = 55° and ∠PSR = 82°, calculate:
1) ∠QRS
2) ∠RQS
3) ∠PRQ

In a cyclic quadrilateral ABCD, the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
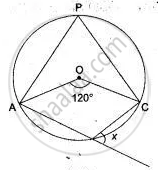
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC = 120°.
Calculate:
- ∠BEC
- ∠BED
In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°.

Find:
- ∠CAD
- ∠CBD
- ∠ADC
In following figure , O is the centre of the circle. If ∠ APB = 50° then find ∠ AOB and ∠ OAB.

In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65° , find the remaining angles.
In triangle ABC, AB = AC. A circle passing through B and c intersects the sides AB and AC at D and E respectively. Prove that DE || BC.
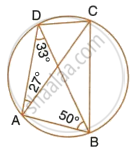
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate : ∠CAB.
ABCD is a parallelogram. A circle through vertices A and B meets side BC at point P and side AD at point Q. Show that quadrilateral PCDQ is cyclic.
If O is the centre of the circle, find the value of x in each of the following figures