Advertisements
Advertisements
प्रश्न
In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°.

Find:
- ∠CAD
- ∠CBD
- ∠ADC
उत्तर
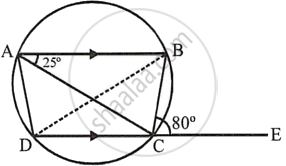
In the given figure,
ABCD is a cyclic quad in which AB || DC
∴ ABCD is an isosceles trapezium
∴ AD = BC
i. Join BD
Ext. ∠BCE = ∠BAD ...[Exterior angle of a cyclic qud is equal to interior opposite angle]
∴ ∠BAD = 80° ...[∵ ∠BCE = 80°]
But ∠BAC = 25°
∴ ∠CAD = ∠BAD – ∠BAC
= 80° – 25°
= 55°
ii. ∠CBD = ∠CAD ...[Angle of the same segment]
= 55°
iii. ∠ADC = ∠BCD ...[Angles of the isosceles trapezium]
= 180° – ∠BCE
= 180° – 80°
= 100°
APPEARS IN
संबंधित प्रश्न
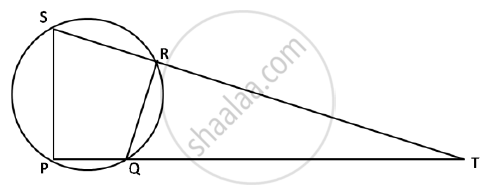
In the given figure PQRS is a cyclic quadrilateral PQ and SR produced meet at T
1) Prove ΔTPS ~ ΔTRQ.
2) Find SP if TP = 18 cm, RQ = 4 cm and TR = 6 cm
3) Find the area of quadrilateral PQRS if the area of ΔPTS = 27 cm2.
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°.
Calculate:
- ∠DBC,
- ∠DCB,
- ∠CAB.

In cyclic quadrilateral ABCD, ∠A = 3∠C and ∠D = 5∠B. Find the measure of each angle of the quadrilateral.
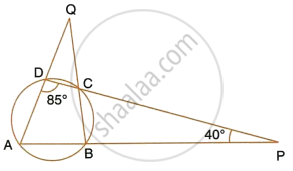
Use the given figure to find:
- ∠BAD,
- ∠DQB.
Bisectors of vertex angles A, B, and C of a triangle ABC intersect its circumcircle at the points D, E and F respectively. Prove that angle EDF = 90° – `1/2` ∠A.
Prove that the angles bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (provided they are not parallel) intersect at right triangle.
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of Δ DEF are 90° - `"A"/2` , 90° - `"B"/2` and 90° - `"C"/2` respectively.
In following fig., O is the centre of the circle. Find ∠ CBD.
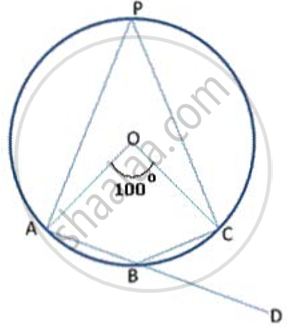
In the figure, given below, find: ∠ABC. Show steps of your working.

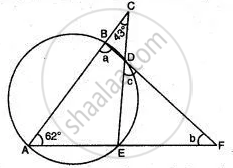
In the given figure, if ∠ ACE = 43° and ∠CAF = 62°. Find the value of a, b, and c.