Advertisements
Advertisements
प्रश्न
Prove that the angles bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (provided they are not parallel) intersect at right triangle.
उत्तर
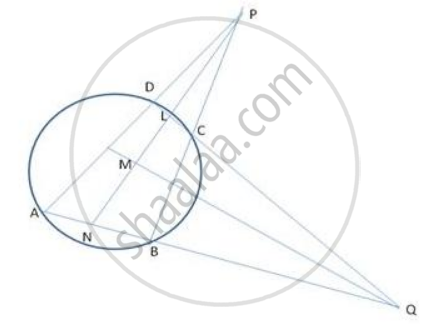
Here, ABCD is a cyclic quadrilateral. PM is bisector of ∠ APB and QM is bisector of ∠ AQD
In Δ PDL and Δ PBN, ∠ 1=∠ 2 (PM is a bisector of LP)
∠ 3 = ∠ 9 (exterior angle of cydic quad. = interior opposite angle)
∴ ∠ 4 = ∠ 7
But, ∠ 4 = ∠ 8 (vertical opposite angles)
∴ ∠ 7 = ∠ 8
Now in Δ QMN and Δ QML
∠ 7 = ∠ 8 (proved above)
∠ S = ∠ 6 (QM is bisector of Q)
∴ Δ QMN ~ Δ QML
⇒ ∠ QMN and ∠ QML
But, ∠ QMN + ∠ QML = 180°
∴ ∠ QMN = ∠ QML = 90°
Hence, ∠ PMQ = 90 °
APPEARS IN
संबंधित प्रश्न
In the following figure,
- if ∠BAD = 96°, find ∠BCD and ∠BFE.
- Prove that AD is parallel to FE.

In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If ∠BCG = 108° and O is the centre of the circle, find :
- angle BCT
- angle DOC

ABCD is a cyclic quadrilateral in which BC is parallel to AD, angle ADC = 110° and angle BAC = 50°. Find angle DAC and angle DCA.
D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Prove that the points B, C, E and D are concyclic.
In following figure , Δ PQR is an isosceles teiangle with PQ = PR and m ∠ PQR = 35° .Find m ∠ QSR and ∠ QTR

ABCD is a parallelogram. A circle through vertices A and B meets side BC at point P and side AD at point Q. Show that quadrilateral PCDQ is cyclic.
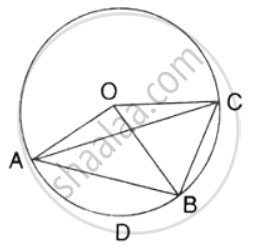
In the figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC. If angle AOB = 108°, find: ∠ADB.
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BDC
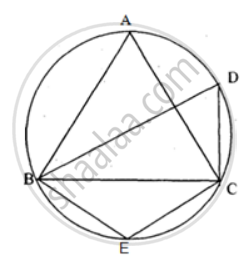
In Fig. ABCD is a cyclic quadrilateral. A circle passing through A and B meets AD and BC in the points E and F respectively. Prove that EF || DC.
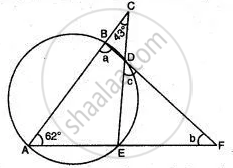
In the given figure, if ∠ ACE = 43° and ∠CAF = 62°. Find the value of a, b, and c.