Advertisements
Advertisements
प्रश्न
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of Δ DEF are 90° -
उत्तर
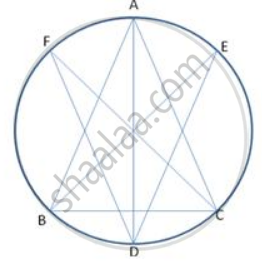
Since AD , BE and CF are bisectors of ∠ A , ∠ B and ∠ C respectively.
∴ ∠1 = ∠ 2 = ∠
∠3 = ∠4 = ∠
∠5= ∠6 = ∠
∠ADE = ∠3 ....(1)
Also ∠ADF = ∠6 ....(2) (angles in the same segment)
Adding (1) and (2)
∠ADE + ∠ADF = ∠3 + ∠6
∠D =
∠D =
∠D = 90 -
Similarly ,
∠E = 90 -
APPEARS IN
संबंधित प्रश्न
In the figure, given below, find:
- ∠BCD,
- ∠ADC,
- ∠ABC.
Show steps of your working.

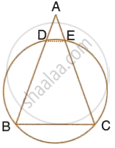
In the given figure, AB = AC. Prove that DECB is an isosceles trapezium.
Prove that any four vertices of a regular pentagon are concylic (lie on the same circle).
In the given figure, O is the centre of the circle. The tangents at B and D intersect each other at point P. If AB is parallel to CD and ∠ABC = 55°, find:
- ∠BOD
- ∠BPD
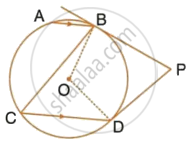
ABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB = 60°.
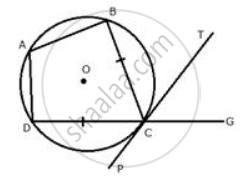
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If angle BCG=108° and O is the centre of the circle, find: angle DOC
In the given below the figure, O is the centre of the circle and ∠ AOC = 160°. Prove that 3∠y - 2∠x = 140°.

ABCD is a cyclic quadrilateral AB and DC are produced to meet in E. Prove that Δ EBC ∼ Δ EDA.
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

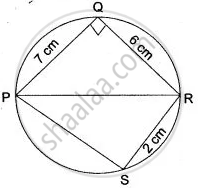
In the figure alongside PR is a diameter of the circle, PQ = 7 cm; QR = 6 cm and RS = 2 cm. Calculate the perimeter of the cyclic quadrilateral PQRS.