Advertisements
Advertisements
प्रश्न
In the given figure, ∠ACE = 43° and ∠CAF = 62°; find the values of a, b and c.

उत्तर
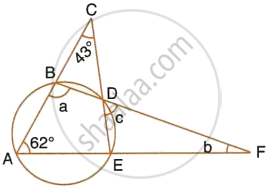
Now, ∠ACE = 43° and ∠CAF = 62° ...[Given]
In ΔAEC
∴ ∠ACE + ∠CAE + ∠AEC = 180°
`=>` 43° + 62° + ∠AEC = 180°
`=>` 105° + ∠AEC = 180°
`=>` ∠AEC = 180° – 105° = 75°
Now, ∠ABD + ∠AED = 180° ...[Opposite angles of a cyclic quad and ∠AED = ∠AEC]
`=>` a + 75° = 180°
`=>` a = 180° – 75°
`=>` a = 105°
∠EDF = ∠BAF
∴ c = 62° ...[Angles in the alternate segments]
In ΔBAF, a + 62° + b = 180°
`=>` 105° + 62° + b = 180°
`=>` 167° + b = 180°
`=>` b = 180° – 167° = 13°
Hence, a = 105°, b = 13° and c = 62°.
APPEARS IN
संबंधित प्रश्न
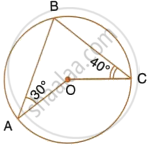
In the given figure, O is the centre of the circle. ∠OAB and ∠OCB are 30° and 40° respectively. Find ∠AOC . Show your steps of working.
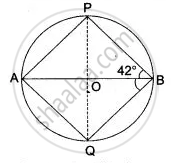
The given figure shows a circle with centre O and ∠ABP = 42°.

Calculate the measure of:
- ∠PQB
- ∠QPB + ∠PBQ
If two sides of a cyclic quadrilateral are parallel; prove that:
- its other two sides are equal.
- its diagonals are equal.
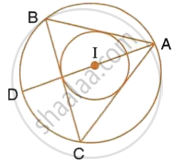
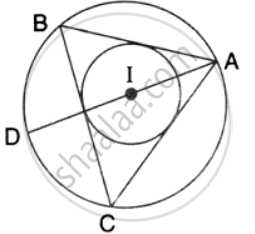
If I is the incentre of triangle ABC and AI when produced meets the circumcircle of triangle ABC in point D. If ∠BAC = 66° and ∠ABC = 80°.
Calculate:
- ∠DBC,
- ∠IBC,
- ∠BIC.
In the given figure, AB = AD = DC = PB and ∠DBC = x°. Determine, in terms of x :
- ∠ABD,
- ∠APB.
Hence or otherwise, prove that AP is parallel to DB.
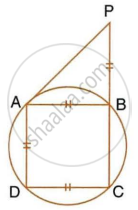
AB is a diameter of the circle APBR, as shown in the figure. APQ and RBQ are straight lines. Find : ∠BPR
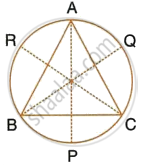
A triangle ABC is inscribed in a circle. The bisectors of angles BAC, ABC and ACB meet the circumcircle of the triangle at points P, Q and R respectively. Prove that :
`∠QPR = 90^circ - 1/2 ∠BAC`
If I is the incentre of triangle ABC and AI when produced meets the cicrumcircle of triangle ABC in points D. f ∠BAC = 66° and ∠ABC = 80°. Calculate : ∠BIC.
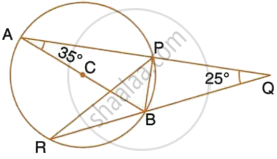
In the following figure, O is the centre of the circle, ∠ PBA = 42°.
Calculate:
(i) ∠ APB
(ii) ∠PQB
(iii) ∠ AQB
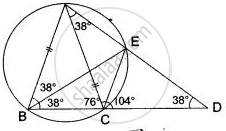
In the figure, AB = AC = CD, ∠ADC = 38°. Calculate: (i) ∠ ABC, (ii) ∠ BEC.