Advertisements
Advertisements
प्रश्न
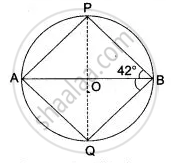
In the following figure, O is the centre of the circle, ∠ PBA = 42°.
Calculate:
(i) ∠ APB
(ii) ∠PQB
(iii) ∠ AQB
उत्तर
(i) In circle C(O, r)
AB is the diameter.
So, ∠ APB = 90° ....(Angle in a semicircle)
(ii) Now in Δ APB,
∠ PAB = 180° - (∠ APB + ∠ ABP)
∠ PAB = 180° - ( 90° + 42°)
∠ PAB = 180° - 132°
∠ PAB = 48°
∠ PQB = ∠ PAB = 48° ....(Angle of the same segment)
Hence,
∠ PQB = 48°
(iii) AQBP is a cyclic quadrilateral.
∠ APB + ∠ AQB = 180°
⇒ 90° + ∠ AQB = 180°
⇒ ∠ AQB = 180° - 90° = 90°.
APPEARS IN
संबंधित प्रश्न
In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°
- Prove that AC is a diameter of the circle.
- Find ∠ACB.

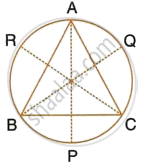
A triangle ABC is inscribed in a circle. The bisectors of angles BAC, ABC and ACB meet the circumcircle of the triangle at points P, Q and R respectively. Prove that:
- ∠ABC = 2∠APQ,
- ∠ACB = 2∠APR,
- `∠QPR = 90^circ - 1/2 ∠BAC`.
The given figure shows a circle with centre O and ∠ABP = 42°.

Calculate the measure of:
- ∠PQB
- ∠QPB + ∠PBQ
In a cyclic-trapezium, the non-parallel sides are equal and the diagonals are also equal. Prove it.
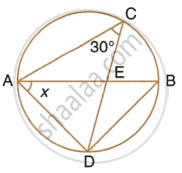
In the given circle with diameter AB, find the value of x.
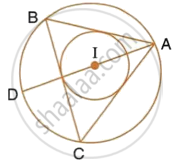
If I is the incentre of triangle ABC and AI when produced meets the circumcircle of triangle ABC in point D. If ∠BAC = 66° and ∠ABC = 80°.
Calculate:
- ∠DBC,
- ∠IBC,
- ∠BIC.
In the given figure, AB = AD = DC = PB and ∠DBC = x°. Determine, in terms of x :
- ∠ABD,
- ∠APB.
Hence or otherwise, prove that AP is parallel to DB.
In the figure given alongside, AB and CD are straight lines through the centre O of a circle. If ∠AOC = 80° and ∠CDE = 40°, find the number of degrees in ∠ABC.

In the given figure, ∠CAB = 25°, find ∠BDC, ∠DBA and ∠COB
In the given figure (drawn not to scale) chords AD and BC intersect at P, where AB = 9 cm, PB = 3 cm and PD = 2 cm.
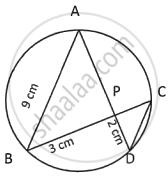
- Prove that ΔAPB ~ ΔCPD.
- Find the length of CD.
- Find area ΔAPB : area ΔCPD.
