Advertisements
Advertisements
प्रश्न
In the given figure (drawn not to scale) chords AD and BC intersect at P, where AB = 9 cm, PB = 3 cm and PD = 2 cm.
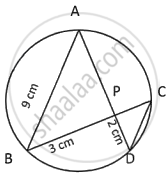
- Prove that ΔAPB ~ ΔCPD.
- Find the length of CD.
- Find area ΔAPB : area ΔCPD.
उत्तर
a. In ΔAPB and ΔCPD,
∠BAP = ∠DCP ...(∠s on same segment)
∠ABP = ∠CDP ...(∠s on same segment)
∴ ΔAPB ~ ΔCPD ...(AA axiom)
b. `(AB)/(CD) = 3/2`
∴ CD = 6 cm
c. `(Area (ΔAPB))/(Area ΔCPD) = (BP^2)/(DP^2)`
= `9/4`
`\implies` 9 : 4
APPEARS IN
संबंधित प्रश्न
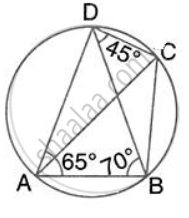
In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°
- Prove that AC is a diameter of the circle.
- Find ∠ACB.

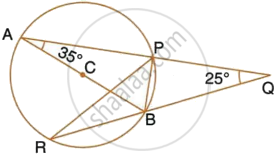
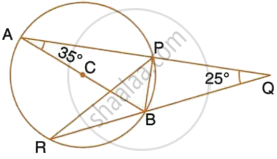
AB is a diameter of the circle APBR as shown in the figure. APQ and RBQ are straight lines. Find : ∠PRB
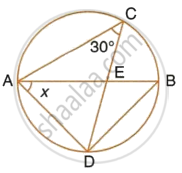
In the given circle with diameter AB, find the value of x.
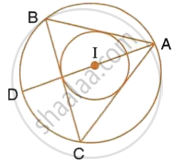
If I is the incentre of triangle ABC and AI when produced meets the circumcircle of triangle ABC in point D. If ∠BAC = 66° and ∠ABC = 80°.
Calculate:
- ∠DBC,
- ∠IBC,
- ∠BIC.
AB is a diameter of the circle APBR as shown in the figure. APQ and RBQ are straight lines. Find : ∠PBR
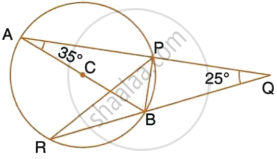
AB is a diameter of the circle APBR, as shown in the figure. APQ and RBQ are straight lines. Find : ∠BPR
In the given figure, ∠BAD = 65°, ∠ABD = 70° and ∠BDC = 45°. Find: ∠ ACB.
Hence, show that AC is a diameter.
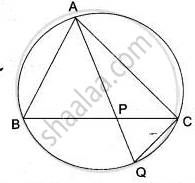
In the given Figure. P is any point on the chord BC of a circle such that AB = AP. Prove that CP = CQ.
In the given below the figure, AB is parallel to DC, ∠BCD = 80° and ∠BAC = 25°, Find
(i) ∠CAD, (ii) ∠CBD, (iii) ∠ADC.

In the given figure, ∠CAB = 25°, find ∠BDC, ∠DBA and ∠COB
