Advertisements
Advertisements
प्रश्न
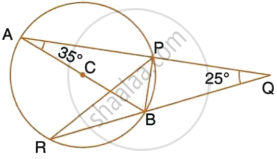
AB is a diameter of the circle APBR as shown in the figure. APQ and RBQ are straight lines. Find : ∠PBR
उत्तर

∠BPA = 90°
(Angle in a semicircle is a right angle)
∴ ∠BPQ = 90°
∴ ∠PBR = ∠BQP + ∠BPQ
= 25° + 90°
= 115°
(Exterior angle of a ∆ is equal to the sum of pair of interior opposite angles)
APPEARS IN
संबंधित प्रश्न
In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°
- Prove that AC is a diameter of the circle.
- Find ∠ACB.

A triangle ABC is inscribed in a circle. The bisectors of angles BAC, ABC and ACB meet the circumcircle of the triangle at points P, Q and R respectively. Prove that:
- ∠ABC = 2∠APQ,
- ∠ACB = 2∠APR,
- `∠QPR = 90^circ - 1/2 ∠BAC`.
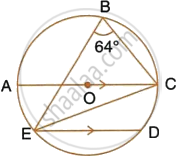
In the given figure, AOC is a diameter and AC is parallel to ED. If ∠CBE = 64°, calculate ∠DEC.
In a cyclic-trapezium, the non-parallel sides are equal and the diagonals are also equal. Prove it.
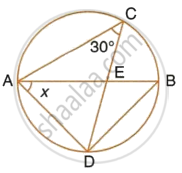
In the given circle with diameter AB, find the value of x.
In the given figure, AB = AD = DC = PB and ∠DBC = x°. Determine, in terms of x :
- ∠ABD,
- ∠APB.
Hence or otherwise, prove that AP is parallel to DB.
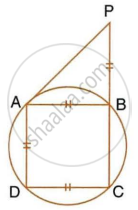
In the figure, given below, CP bisects angle ACB. Show that DP bisects angle ADB.

In the figure, given below, AD = BC, ∠BAC = 30° and ∠CBD = 70°.
Find:
- ∠BCD
- ∠BCA
- ∠ABC
- ∠ADB
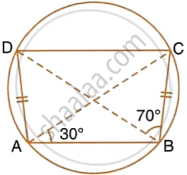
In the given figure, ∠BAD = 65°, ∠ABD = 70° and ∠BDC = 45°. Find: ∠ ACB.
Hence, show that AC is a diameter.
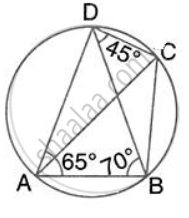
In the given figure, ∠CAB = 25°, find ∠BDC, ∠DBA and ∠COB
