Advertisements
Advertisements
प्रश्न
AB is a diameter of the circle APBR as shown in the figure. APQ and RBQ are straight lines. Find : ∠PRB
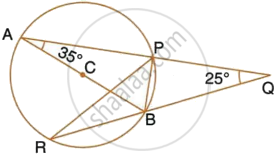
उत्तर
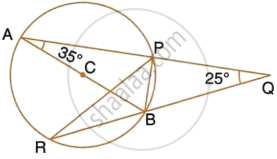
∠PRB = ∠PAB = 35°
(Angles subtended by the same chord on the circle are equal)
APPEARS IN
संबंधित प्रश्न
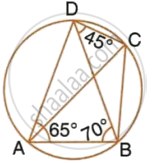
In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°
- Prove that AC is a diameter of the circle.
- Find ∠ACB.

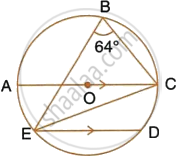
In the given figure, AOC is a diameter and AC is parallel to ED. If ∠CBE = 64°, calculate ∠DEC.
In the given figure, ∠BAD = 65°, ∠ABD = 70° and ∠BDC = 45°. Find:
- ∠BCD
- ∠ACB
Hence, show that AC is a diameter.
If two sides of a cyclic quadrilateral are parallel; prove that:
- its other two sides are equal.
- its diagonals are equal.
In cyclic quadrilateral ABCD; AD = BC, ∠BAC = 30° and ∠CBD = 70°; find:
- ∠BCD
- ∠BCA
- ∠ABC
- ∠ADC
In the figure, given below, CP bisects angle ACB. Show that DP bisects angle ADB.

A triangle ABC is inscribed in a circle. The bisectors of angles BAC, ABC and ACB meet the circumcircle of the triangle at points P, Q and R respectively. Prove that :
∠ACB = 2∠APR,
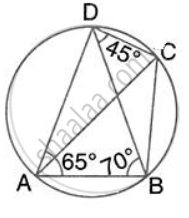
In the given figure, ∠BAD = 65°, ∠ABD = 70° and ∠BDC = 45°. Find: ∠ ACB.
Hence, show that AC is a diameter.
If I is the incentre of triangle ABC and AI when produced meets the cicrumcircle of triangle ABC in points D. f ∠BAC = 66° and ∠ABC = 80°. Calculate : ∠BIC.
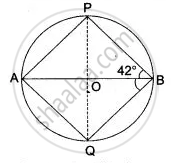
In the following figure, O is the centre of the circle, ∠ PBA = 42°.
Calculate:
(i) ∠ APB
(ii) ∠PQB
(iii) ∠ AQB