Advertisements
Advertisements
प्रश्न
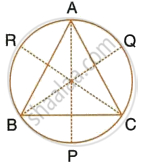
A triangle ABC is inscribed in a circle. The bisectors of angles BAC, ABC and ACB meet the circumcircle of the triangle at points P, Q and R respectively. Prove that :
∠ACB = 2∠APR,
उत्तर
Join PQ and PR
CR is the bisector of ∠ACB
`=> ∠ACR = 1/2 ∠ACB`
Also, ∠ACR = ∠APR
(Angle in the same segment)
∴ ∠ACB = 2∠APR
APPEARS IN
संबंधित प्रश्न
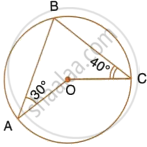
In the given figure, O is the centre of the circle. ∠OAB and ∠OCB are 30° and 40° respectively. Find ∠AOC . Show your steps of working.
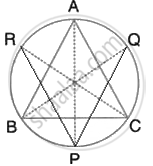
A triangle ABC is inscribed in a circle. The bisectors of angles BAC, ABC and ACB meet the circumcircle of the triangle at points P, Q and R respectively. Prove that:
- ∠ABC = 2∠APQ,
- ∠ACB = 2∠APR,
- `∠QPR = 90^circ - 1/2 ∠BAC`.
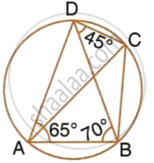
In the given figure, ∠BAD = 65°, ∠ABD = 70° and ∠BDC = 45°. Find:
- ∠BCD
- ∠ACB
Hence, show that AC is a diameter.
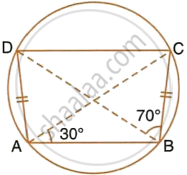
In the figure, given below, AD = BC, ∠BAC = 30° and ∠CBD = 70°.
Find:
- ∠BCD
- ∠BCA
- ∠ABC
- ∠ADB
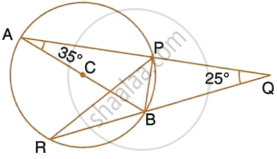
AB is a diameter of the circle APBR as shown in the figure. APQ and RBQ are straight lines. Find : ∠PBR
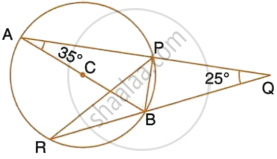
AB is a diameter of the circle APBR, as shown in the figure. APQ and RBQ are straight lines. Find : ∠BPR
If I is the incentre of triangle ABC and AI when produced meets the cicrumcircle of triangle ABC in points D . if ∠BAC = 66° and ∠ABC = 80°. Calculate : ∠IBC
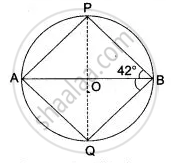
In the following figure, O is the centre of the circle, ∠ PBA = 42°.
Calculate:
(i) ∠ APB
(ii) ∠PQB
(iii) ∠ AQB
In the given figure, ∠CAB = 25°, find ∠BDC, ∠DBA and ∠COB
In the given figure (drawn not to scale) chords AD and BC intersect at P, where AB = 9 cm, PB = 3 cm and PD = 2 cm.
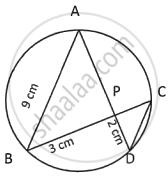
- Prove that ΔAPB ~ ΔCPD.
- Find the length of CD.
- Find area ΔAPB : area ΔCPD.
