Advertisements
Advertisements
प्रश्न
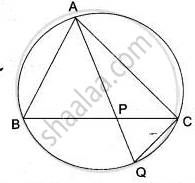
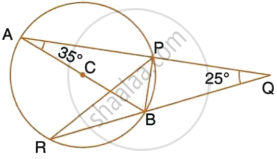
In the given Figure. P is any point on the chord BC of a circle such that AB = AP. Prove that CP = CQ.
उत्तर
We have to prove that CP = CQ i.e., Δ CPQ is an isosceles triangle. for this it is sufficient to prove that ∠ CPQ = ∠ CQP.
In Δ ABP, we have
AB = AP
⇒ ∠ APB = ∠ ABP
⇒ ∠ CPQ = ∠ ABP ...(i)( ∵ ∠APB and ∠ CPQ are vertically opposite angles ∴ ∠APB = ∠ CPQ )
Now consider arc AC. Clearly, it subtends ∠ABC and ∠AQC at points B and Q.
∴ ∠ABC = ∠AQC ...( ∵ Angles in the same segment)
⇒ ∠ABP = ∠PQC ...( ∵∠ ABC = ∠ ABP and ∠AQC = ∠PQC )
⇒ ∠ABP = ∠CQP ....(ii)( ∵ ∠PQC = ∠CQP )
From (i) and (ii), we get
∠ CPQ = ∠CQP
⇒ CQ = CP
Hence proved.
APPEARS IN
संबंधित प्रश्न
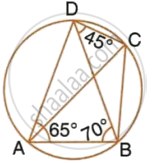
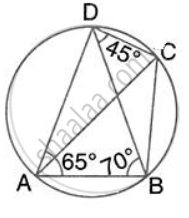
In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°
- Prove that AC is a diameter of the circle.
- Find ∠ACB.

In the given figure, ∠BAD = 65°, ∠ABD = 70° and ∠BDC = 45°. Find:
- ∠BCD
- ∠ACB
Hence, show that AC is a diameter.
In a cyclic-trapezium, the non-parallel sides are equal and the diagonals are also equal. Prove it.
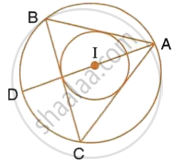
If I is the incentre of triangle ABC and AI when produced meets the circumcircle of triangle ABC in point D. If ∠BAC = 66° and ∠ABC = 80°.
Calculate:
- ∠DBC,
- ∠IBC,
- ∠BIC.
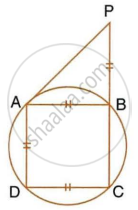
In the given figure, AB = AD = DC = PB and ∠DBC = x°. Determine, in terms of x :
- ∠ABD,
- ∠APB.
Hence or otherwise, prove that AP is parallel to DB.
In cyclic quadrilateral ABCD; AD = BC, ∠BAC = 30° and ∠CBD = 70°; find:
- ∠BCD
- ∠BCA
- ∠ABC
- ∠ADC
In the figure given alongside, AB and CD are straight lines through the centre O of a circle. If ∠AOC = 80° and ∠CDE = 40°, find the number of degrees in ∠ABC.

AB is a diameter of the circle APBR as shown in the figure. APQ and RBQ are straight lines. Find : ∠PBR
In the given figure, ∠BAD = 65°, ∠ABD = 70° and ∠BDC = 45°. Find: ∠ ACB.
Hence, show that AC is a diameter.
In the given below the figure, AB is parallel to DC, ∠BCD = 80° and ∠BAC = 25°, Find
(i) ∠CAD, (ii) ∠CBD, (iii) ∠ADC.

