Advertisements
Advertisements
Question
In the given Figure. P is any point on the chord BC of a circle such that AB = AP. Prove that CP = CQ.
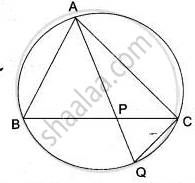
Solution
We have to prove that CP = CQ i.e., Δ CPQ is an isosceles triangle. for this it is sufficient to prove that ∠ CPQ = ∠ CQP.
In Δ ABP, we have
AB = AP
⇒ ∠ APB = ∠ ABP
⇒ ∠ CPQ = ∠ ABP ...(i)( ∵ ∠APB and ∠ CPQ are vertically opposite angles ∴ ∠APB = ∠ CPQ )
Now consider arc AC. Clearly, it subtends ∠ABC and ∠AQC at points B and Q.
∴ ∠ABC = ∠AQC ...( ∵ Angles in the same segment)
⇒ ∠ABP = ∠PQC ...( ∵∠ ABC = ∠ ABP and ∠AQC = ∠PQC )
⇒ ∠ABP = ∠CQP ....(ii)( ∵ ∠PQC = ∠CQP )
From (i) and (ii), we get
∠ CPQ = ∠CQP
⇒ CQ = CP
Hence proved.
APPEARS IN
RELATED QUESTIONS
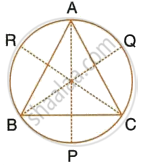
A triangle ABC is inscribed in a circle. The bisectors of angles BAC, ABC and ACB meet the circumcircle of the triangle at points P, Q and R respectively. Prove that:
- ∠ABC = 2∠APQ,
- ∠ACB = 2∠APR,
- `∠QPR = 90^circ - 1/2 ∠BAC`.
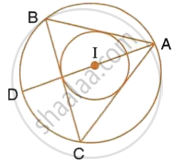
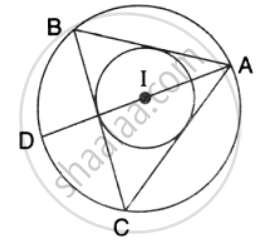
If I is the incentre of triangle ABC and AI when produced meets the circumcircle of triangle ABC in point D. If ∠BAC = 66° and ∠ABC = 80°.
Calculate:
- ∠DBC,
- ∠IBC,
- ∠BIC.
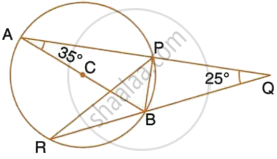
In the given figure, ∠ACE = 43° and ∠CAF = 62°; find the values of a, b and c.

In the figure, given below, CP bisects angle ACB. Show that DP bisects angle ADB.

In the figure given alongside, AB and CD are straight lines through the centre O of a circle. If ∠AOC = 80° and ∠CDE = 40°, find the number of degrees in ∠ABC.

AB is a diameter of the circle APBR, as shown in the figure. APQ and RBQ are straight lines. Find : ∠BPR
A triangle ABC is inscribed in a circle. The bisectors of angles BAC, ABC and ACB meet the circumcircle of the triangle at points P, Q and R respectively. Prove that :
∠ACB = 2∠APR,
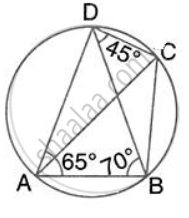
In the given figure, ∠BAD = 65°, ∠ABD = 70° and ∠BDC = 45°. Find: ∠ ACB.
Hence, show that AC is a diameter.
If I is the incentre of triangle ABC and AI when produced meets the cicrumcircle of triangle ABC in points D . if ∠BAC = 66° and ∠ABC = 80°. Calculate : ∠IBC
In the given figure (drawn not to scale) chords AD and BC intersect at P, where AB = 9 cm, PB = 3 cm and PD = 2 cm.
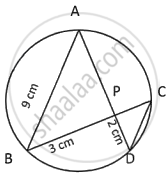
- Prove that ΔAPB ~ ΔCPD.
- Find the length of CD.
- Find area ΔAPB : area ΔCPD.
