(English Medium)
Academic Year: 2024-2025
Date: अप्रैल 2025
Advertisements
- Answers to this Paper must be written on the paper provided separately.
- You will not be allowed to write during first 15 minutes.
- This time is to be spent in reading the question paper.
- The time given at the head of this Paper is the time allowed for writing the answers.
- Attempt all questions from Section A and any four questions from Section B.
- All working, including rough work, must be clearly shown, and must be done on the same sheet as the rest of the answer.
- Omission of essential working will result in loss of marks.
- The intended marks for questions or parts of questions are given in brackets [ ]
- Mathematical tables are provided.
A polynomial in ‘x’ is divided by (x – a) and for (x – a) to be a factor of this polynomial, the remainder should be ______.
– a
0
a
2a
Chapter: [0.08] Factorization
Radha deposited ₹ 400 per month in a recurring deposit account for 18 months. The qualifying sum of money for the calculation of interest is ______.
₹ 3600
₹ 7200
₹ 68,400
₹ 1,36,800
Chapter: [0.02] Banking
In the adjoining figure, AC is a diameter of the circle. AP = 3 cm and PB = 4 cm and QP ⊥ AB. If the area of ΔAPQ is 18 cm2, then the area of shaded portion QPBC is ______.
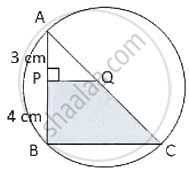
32 cm2
49 cm2
80 cm2
98 cm2
Chapter: [0.17] Circles
In the adjoining diagram, O is the centre of the circle and PT is a tangent. The value of x is ______.
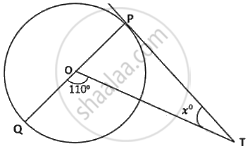
20°
40°
55°
70°
Chapter: [0.17] Circles
In the adjoining diagram the length of PR is ______.

`3sqrt(3)` cm
`6sqrt(3)` cm
`9sqrt(3)` cm
18 cm
Chapter: [0.15] Similarity
A solid sphere is cut into two identical hemispheres.
Statement 1: The total volume of two hemispheres is equal to the volume of the original sphere.
Statement 2: The total surface area of two hemispheres together is equal to the surface area of the original sphere.
Which of the following is valid?
Both the statements are true.
Both the statements are false.
Statement 1 is true and Statement 2 is false.
Statement 1 is false and Statement 2 is true.
Chapter: [0.04] Mensuration [0.04] Mensuration
Given that the sum of the squares of the first seven natural numbers is 140, then their mean is ______.
20
70
280
980
Chapter: [0.06] Solving (Simple) Problems (Based on Quadratic Equations)
A bag contains 3 red and 2 blue marbles. A marble is drawn at random. ‘The probability of drawing a black marble is ______.
0
`1/5`
`2/5`
`3/5`
Chapter: [0.07] Probability
If A = `[(3, -2)]` and B = `[(-1, 4),(2, 0)]`
Assertion (A): Product AB of the two matrices A and B is possible.
Reason (R): Number of columns of matrix A is equal to number of rows in matrix B.
A is true, R is false.
A is false, R is true.
Both A and R are true and R is the correct reason for A.
Both A and R are true and R is incorrect reason for A.
Chapter: [0.09] Matrices
A mixture of paint is prepared by mixing 2 parts of red pigments with 5 parts of the base. Using the given information in the following table, find the values of a, b and c to get the required mixture of paint.
| Parts of red pigment | 2 | 4 | b | 6 |
| Parts of base | 5 | a | 12.5 | c |
a = 10, b = 10, c = 10
a = 5, b = 2, c = 5
a = 10, b = 5, c = 10
a = 10, b = 5, c = 15
Chapter: [0.07] Ratio and Proportion
An article which is marked at ₹ 1200 is available at a discount of 20% and the rate of GST is 18%. The amount of SGST is ______.
₹ 216.00
₹ 172.80
₹ 108.00
₹ 86.40
Chapter: [0.01] GST (Goods and Services Tax)
The sum of money required to buy 50, ₹ 40 shares at ₹ 38.50 is ______.
₹ 1920
₹ 1924
₹ 1925
₹ 1952
Chapter: [0.03] Shares and Dividends
The roots of quadratic equation x2 – 1 = 0 are ______.
0
1
–1
±1
Chapter: [0.05] Quadratic Equations
Which of the following equation represents a line equally inclined to the axes?
2x – 3y + 7 = 0
x – y = 7
x = 7
y = –7
Chapter: [0.14] Co-ordinate Geometry Equation of a Line
Given, `x + 2 ≤ x/3 + 3` and x is a prime number. The solution set for x is ______.
∅
{0}
{1}
{0, 1}
Chapter: [0.04] Linear Inequations
Advertisements
While factorizing a given polynomial, using remainder and factor theorem, a student finds that (2x + 1) is a factor of 2x3 + 7x2 + 2x – 3.
- Is the student's solution correct stating that (2x + 1) is a factor of the given polynomial?
- Give a valid reason for your answer.
Also, factorize the given polynomial completely.
Chapter: [0.08] Factorization
A line segment joining P(2, –3) and Q(0, –1) is cut by the x-axis at the point R. A line AB cuts the y-axis at T(0, 6) and is perpendicular to PQ at S.
Find the:
- equation of line PQ
- equation of line AB
- coordinates of points R and S.
Chapter: [0.14] Co-ordinate Geometry Equation of a Line
In the given figure AC is the diameter of the circle with centre O. CD is parallel to BE.
∠AOB = 80° and ∠ACE = 20°.
Calculate
- ∠BEC
- ∠BCD
- ∠CED
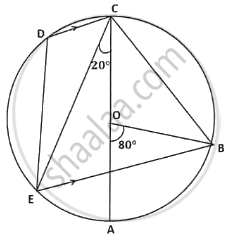
Chapter: [0.17] Circles
In a Geometric Progression (G.P.) the first term is 24 and the fifth term is 8. Find the ninth term of the G.P.
Chapter: [0.11] Geometric Progression
In the adjoining diagram, a tilted right circular cylindrical vessel with base diameter 7 cm contains a liquid. When placed vertically, the height of the liquid in the vessel is the mean of two heights shown in the diagram. Find the area of wet surface, when the cylinder is placed vertically on a horizontal surface. (Use π = `22/7`).
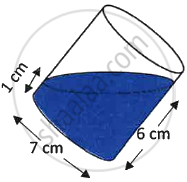
Chapter: [0.04] Mensuration
Study the graph and answer each of the following:
- Write the coordinates of points A, B, C and D.
- Given that, point C is the image of point A. Name and write the equation of the line of reflection.
- Write the coordinates of the image of the point D under reflection in y-axis.
- Whats the name given to a point whose image is the point itself?
- On joining the points A, B, C, D and A in order, a figure is formed. Name the closed figure.
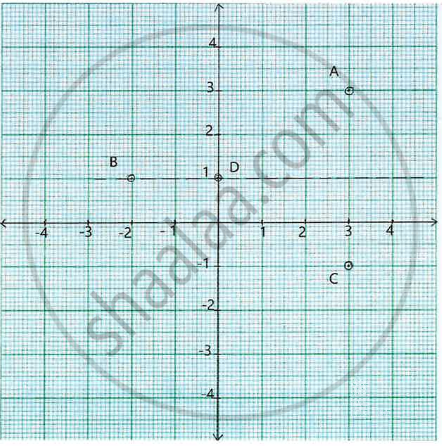
Chapter: [0.12] Reflection
A man buys 250, ten-rupee shares each at ₹ 12.50. If the rate of dividend is 7%, find the:
- dividend he receives annually.
- percentage return on his investment.
Chapter: [0.03] Shares and Dividends
Solve the following inequation, write the solution set and represent it on the real number line.
`5x - 21 < (5x)/7 - 6 ≤ -3 3/7 + x, x ∈ R`
Chapter: [0.04] Linear Inequations
Prove the following trigonometry identity:
(sinθ + cosθ)(cosecθ – secθ) = cosecθ.secθ – 2 tanθ
Chapter: [0.05] Trigonometry
In the given figure (drawn not to scale) chords AD and BC intersect at P, where AB = 9 cm, PB = 3 cm and PD = 2 cm.
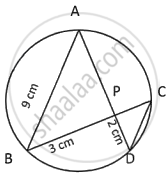
- Prove that ΔAPB ~ ΔCPD.
- Find the length of CD.
- Find area ΔAPB : area ΔCPD.
Chapter: [0.17] Circles
Mr. Sameer has a recurring deposit account and deposits ₹ 600 per month for 2 years. If he gets ₹ 15600 at the time of maturity, find the rate of interest earned by him.
Chapter: [0.02] Banking
Using step-deviation method, find mean for the following frequency distribution:
| Class | 0 – 15 | 15 – 30 | 30 – 45 | 45 – 60 | 60 – 75 | 75 – 90 |
| Frequency | 3 | 4 | 7 | 6 | 8 | 2 |
Chapter: [0.06] Statistics
Find the coordinates of the centroid P of the ΔABC, whose vertices are A(–1, 3), B(3, –1) and C(0, 0). Hence, find the equation of a line passing through P and parallel to AB.
Chapter: [0.13] Co-ordinate Geometry Distance and Section Formula
Advertisements
In the given figure PT is a tangent to the circle. Chord BA produced meets the tangent PT at P.
Given PT = 20 cm and PA = 16 cm.
- Prove ΔPTB ~ ΔPAT
- Find the length of AB.
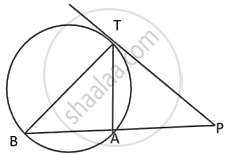
Chapter: [0.17] Circles
The following bill shows the GST rate and the marked price of articles:
| Rajdhani Departmental Store | ||||
| S.No. | Item | Marked Price |
Discount |
Rate of GST |
| (a) | Dry fruits (1 kg) | ₹ 1200 | ₹ 100 | 12% |
| (b) | Packed Wheat flour (5 kg) | ₹ 286 | Nil | 5% |
| (c) | Bakery products | ₹ 500 | 10% | 12% |
Find the total amount to be paid (including GST) for the above bill.
Chapter: [0.01] GST (Goods and Services Tax)
A vertical tower standing on a horizontal plane is surmounted by a vertical flagstaff. At a point 100 m away from the foot of the tower, the angle of elevation of the top and bottom of the flagstaff are 54° and 42° respectively. Find the height of the flagstaff. Give your answer correct to nearest metre.

Chapter: [0.05] Trigonometry
The marks of 200 students in a test were recorded as follows:
| Marks % |
0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
| No. of students |
5 | 7 | 11 | 20 | 40 | 52 | 36 | 15 | 9 | 5 |
Using graph sheet draw ogive for the given data and use it to find the,
- median,
- number of students who obtained more than 65% marks
- number of students who did not pass, if the pass percentage was 35.
Chapter: [0.06] Statistics
In a TV show, a contestant opts for video call a friend life line to get an answer from three of his friends, named Amar, Akbar and Anthony. The question which he asks from one of his friends has four options.
Find the probability that:
- Akbar is chosen for the call.
- Akbar couldn't give the correct answer.
Chapter: [0.07] Probability
If x, y and z are in continued proportion, Prove that:
`x/(y^2.z^2) + y/(z^2.x^2) + z/(x^2.y^2) = 1/x^3 + 1/y^3 + 1/z^3`
Chapter: [0.07] Ratio and Proportion
A manufacturing company prepares spherical ball bearings, each of radius 7 mm and mass 4 gm. These ball bearings are packed into boxes. Each box can have maximum of 2156 cm3 of ball bearings. Find the:
- maximum number of ball bearings that each box can have.
- mass of each box of ball bearings in kg.
(use π = `22/7`)
Chapter: [0.04] Mensuration [0.04] Mensuration
The table given below shows the runs scored by a cricket team during the overs of a match.
| Overs | Runs scored |
| 20 – 30 | 37 |
| 30 – 40 | 45 |
| 40 – 50 | 40 |
| 50 – 60 | 60 |
| 60 – 70 | 51 |
| 70 – 80 | 35 |
Use graph sheet for this question.
Take 2 cm = 10 overs along one axis and 2 cm = 10 runs along the other axis.
- Draw a histogram representing the above distribution.
- Estimate the modal runs scored.
Chapter: [0.06] Statistics [0.06] Statistics
An Arithmetic Progression (A.P.) has 3 as its first term. The sum of the first 8 terms is twice the sum of the first 5 terms. Find the common difference of the A.P.
Chapter: [0.1] Arithmetic Progression
The roots of equation (q – r)x2 + (r – p)x + (p – q) = 0 are equal. Prove that: 2q = p + r, that is, p, q and r are in A.P.
Chapter: [0.05] Quadratic Equations
A car travels a distance of 72 km at a certain average speed of x km per hour and then travels a distance of 81 km at an average speed of 6 km per hour more than its original average speed. If it takes 3 hours to complete the total journey then form a quadratic equation and solve it to find its original average speed.
Chapter: [0.06] Solving (Simple) Problems (Based on Quadratic Equations)
Given matrix, X = `[(1, 1),(8, 3)]` and I = `[(1, 0),(0, 1)]`, prove that X2 = 4X + 5I
Chapter: [0.09] Matrices
Use ruler and compasses for the following question taking a scale of 10 m = 1 cm. A park in a city is bounded by straight fences AB, BC, CD and DA. Given that AB = 50 m, BC = 63 m, ∠ABC = 75°. D is a point equidistant from the fences AB and BC. If ∠BAD = 90°, construct the outline of the park ABCD. Also locate a point P on the line BD for the flag post which is equidistant from the corners of the park A and B.
Chapter: [0.16] Loci
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
CISCE previous year question papers ICSE Class 10 Mathematics with solutions 2024 - 2025
Previous year Question paper for CISCE ICSE Class 10 Maths-2025 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Mathematics, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of CISCE ICSE Class 10 .
How CISCE ICSE Class 10 Question Paper solutions Help Students ?
• Question paper solutions for Mathematics will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.
