Advertisements
Advertisements
प्रश्न
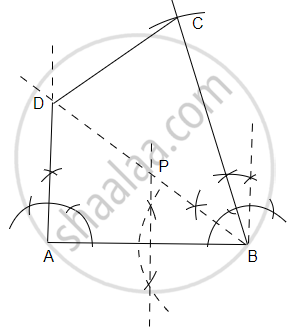
Use ruler and compasses for the following question taking a scale of 10 m = 1 cm. A park in a city is bounded by straight fences AB, BC, CD and DA. Given that AB = 50 m, BC = 63 m, ∠ABC = 75°. D is a point equidistant from the fences AB and BC. If ∠BAD = 90°, construct the outline of the park ABCD. Also locate a point P on the line BD for the flag post which is equidistant from the corners of the park A and B.
उत्तर
APPEARS IN
संबंधित प्रश्न
In triangle LMN, bisectors of interior angles at L and N intersect each other at point A. Prove that:
- Point A is equidistant from all the three sides of the triangle.
- AM bisects angle LMN.
Draw a line AB = 6 cm. Draw the locus of all the points which are equidistant from A and B.
Describe the locus of points at a distance 2 cm from a fixed line.
Describe the locus of a runner, running around a circular track and always keeping a distance of 1.5 m from the inner edge.
Describe the locus of points at distances less than or equal to 2.5 cm from a given point.
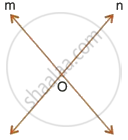
In the given figure, obtain all the points equidistant from lines m and n; and 2.5 cm from O.
In Fig. ABCD is a quadrilateral in which AB = BC. E is the point of intersection of the right bisectors of AD and CD. Prove that BE bisects ∠ABC.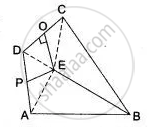
Find the locus of the centre of a circle of radius r touching externally a circle of radius R.
ΔPBC and ΔQBC are two isosceles triangles on the same base BC but on the opposite sides of line BC. Show that PQ bisects BC at right angles.
The bisectors of ∠B and ∠C of a quadrilateral ABCD intersect in P. Show that P is equidistant from the opposite sides AB and CD.
