Advertisements
Advertisements
प्रश्न
Find the locus of the centre of a circle of radius r touching externally a circle of radius R.
उत्तर
Let a circle of radius r (with centre B) touch a circle of radius R at C. Then ACB is a straight line and
AB = AC + CB = R + r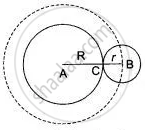
Thus, B moves such that its distance from fixed point. A remains constant and is equal to R + r.
Hence, the locus of B is a circle whose centre is A and radius equal to R + r.
APPEARS IN
संबंधित प्रश्न
Construct a triangle ABC, in which AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm. Draw perpendicular bisector of BC which meets AC at point D. Prove that D is equidistant from B and C.
The given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F.
Prove that:
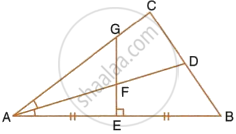
F is equidistant from AB and AC.
Draw a line AB = 6 cm. Draw the locus of all the points which are equidistant from A and B.
Describe the locus for questions 1 to 13 given below:
1. The locus of a point at a distant 3 cm from a fixed point.
Describe the locus of a point in rhombus ABCD, so that it is equidistant from
- AB and BC;
- B and D.
Describe the locus of points at distances greater than 4 cm from a given point.
By actual drawing obtain the points equidistant from lines m and n; and 6 cm from a point P, where P is 2 cm above m, m is parallel to n and m is 6 cm above n.
Find the locus of points which are equidistant from three non-collinear points.
ΔPBC, ΔQBC and ΔRBC are three isosceles triangles on the same base BC. Show that P, Q and R are collinear.
In Fig. AB = AC, BD and CE are the bisectors of ∠ABC and ∠ACB respectively such that BD and CE intersect each other at O. AO produced meets BC at F. Prove that AF is the right bisector of BC.