Advertisements
Online Mock Tests
Chapters
2: Sales Tax and Value Added Tax
3: Banking
4: Shares and Dividends
5: Linear Inequations (Solving Linear Inequations in One Variable)
6: Quadratic Equation
7: Reflection
8: Ratio and Proportion
9: Factorization
10: Matrices
11: Coordinate Geometry
12: Symmetry
13: Similarity
▶ 14: Loci (Locus and its Constructions)
15: Circles
16: Constructions (Circle)
17: Mensuration
18: Trigonometry
19: Statistics
20: Probability
![ICSE solutions for Mathematics [English] Class 10 chapter 14 - Loci (Locus and its Constructions) ICSE solutions for Mathematics [English] Class 10 chapter 14 - Loci (Locus and its Constructions) - Shaalaa.com](/images/mathematics-english-class-10_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
Advertisements
Solutions for Chapter 14: Loci (Locus and its Constructions)
Below listed, you can find solutions for Chapter 14 of CISCE ICSE for Mathematics [English] Class 10.
ICSE solutions for Mathematics [English] Class 10 14 Loci (Locus and its Constructions) Prove the Following
The bisector of ∠ B and ∠C of a quadrilateral ABCD intersect in P, show that P is equidistant from the opposite sides AB and CD.
Prove that the common chord of two intersecting circles is bisected at right angles by the line of centres.
In ΔABC, the bisector AX of ∠A intersects BC ar X. XL ⊥ AB and XM ⊥ AC are drawn (Fig.) is XL = XM? why or why not?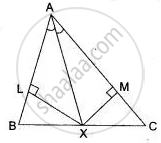
In Fig. ABCD is a quadrilateral in which AB = BC. E is the point of intersection of the right bisectors of AD and CD. Prove that BE bisects ∠ABC.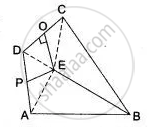
ICSE solutions for Mathematics [English] Class 10 14 Loci (Locus and its Constructions) Figure Based Questions
Without using set squares or protractor, construct a quadrilateral ABCD in which ∠ BAD = 45° , AD = AB = 6 cm, BC= 3.6 cm and CD=5 cm. Locate the point P on BD which is equidistant from BC and CD.
Without using set squares or protractor construct a triangle ABC in which AB = 4 cm, BC = 5 cm and ∠ABC = 120°.
(i) Locate the point P such that ∠BAp = 90° and BP = CP.
(ii) Measure the length of BP.
State and draw the locus of a swimmer maintaining the same distance from a lighthouse.
State and draw the locus of a point equidistant from two given parallel lines.
l is the perpendicular bisector of line segment PQ and R is a point on the same side of l as P. The segment QR intersects l at X. Prove that PX + XR = QR.
Construct a Δ ABC, with AB = 6 cm, AC = BC = 9 cm; find a point 4 cm from A and equidistant from B and C.
Given a Δ ABC with unequal sides. Find a point which is equidistant from B and C as well as from AB and AC.
Prove that the common chord of two intersecting circles is bisected at right angles by the line of centres.
Find the locus of the centre of a circle of radius r touching externally a circle of radius R.
ΔPBC and ΔQBC are two isosceles triangles on the same base. Show that the line PQ is bisector of BC and is perpendicular to BC.
Using a ruler and compass only:
(i) Construct a triangle ABC with BC = 6 cm, ∠ABC = 120° and AB = 3.5 cm.
(ii) In the above figure, draw a circle with BC as diameter. Find a point 'P' on the circumference of the circle which is equidistant from Ab and BC.
Measure ∠BCP.
The diagonals of a quadrilateral bisect each other at right angles. Show that the quadrilateral is a rhombus.
What is the locus of points which are equidistant from the given non-collinear point A, B and C? Justify your answer.
Find the locus of points which are equidistant from three non-collinear points.
Show that the locus of the centres of all circles passing through two given points A and B, is the perpendicular bisector of the line segment AB.
Using ruler and compasses construct:
(i) a triangle ABC in which AB = 5.5 cm, BC = 3.4 cm and CA = 4.9 cm.
(ii) the locus of point equidistant from A and C.
(iii) a circle touching AB at A and passing through C.
Using only a ruler and compass construct ∠ABC = 120°, where AB = BC = 5 cm.
(i) Mark two points D and E which satisfy the condition that they are equidistant from both ABA and BC.
(ii) In the above figure, join AD, DC, AE and EC. Describe the figures:
(a) AECB, (b) ABD, (c) ABE.
ΔPBC and ΔQBC are two isosceles triangles on the same base BC but on the opposite sides of line BC. Show that PQ bisects BC at right angles.
ΔPBC, ΔQBC and ΔRBC are three isosceles triangles on the same base BC. Show that P, Q and R are collinear.
Without using set squares or protractor construct:
(i) Triangle ABC, in which AB = 5.5 cm, BC = 3.2 cm and CA = 4.8 cm.
(ii) Draw the locus of a point which moves so that it is always 2.5 cm from B.
(iii) Draw the locus of a point which moves so that it is equidistant from the sides BC and CA.
(iv) Mark the point of intersection of the loci with the letter P and measure PC.
Use ruler and compasses only for this question. Draw a circle of radius 4 cm and mark two chords AB and AC of the circle of length f 6 cm and 5 cm respectively.
(i) Construct the locus of points, inside the circle, that are equidistant from A and C. Prove your construction.
(ii) Construct the locus of points, inside the circle, that are equidistant from AB and AC.
Draw two intersecting lines to include an angle of 30°. Use ruler and compasses to locate points which are equidistant from these Iines and also 2 cm away from their point of intersection. How many such points exist?
How will you find a point equidistant from three given points A, B, C which are not in the same straight line?
Without using set squares or protractor.
(i) Construct a ΔABC, given BC = 4 cm, angle B = 75° and CA = 6 cm.
(ii) Find the point P such that PB = PC and P is equidistant from the side BC and BA. Measure AP.
In Fig. AB = AC, BD and CE are the bisectors of ∠ABC and ∠ACB respectively such that BD and CE intersect each other at O. AO produced meets BC at F. Prove that AF is the right bisector of BC.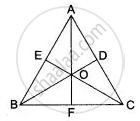
Given: ∠BAC, a line intersects the arms of ∠BAC in P and Q. How will you locate a point on line segment PQ, which is equidistant from AB and AC? Does such a point always exist?
The bisectors of ∠B and ∠C of a quadrilateral ABCD intersect in P. Show that P is equidistant from the opposite sides AB and CD.
Use ruler and compasses only for this question. Draw a circle of radius 4 cm and mark two chords AB and AC of the circle of length f 6 cm and 5 cm respectively.
(i) Construct the locus of points, inside the circle, that are equidistant from A and C. Prove your construction.
(ii) Construct the locus of points, inside the circle, that are equidistant from AB and AC.
Use ruler and compasses only for the following questions:
Construct triangle BCP, when CB = 5 cm, BP = 4 cm, ∠PBC = 45°.
Complete the rectangle ABCD such that :
(i) P is equidistant from AB and BC and
(ii) P is equidistant from C and D. Measure and write down the length of AB.
Ruler and compass only may be used in this question. All construction lines and arcs must be clearly shown, and be of sufficient length and clarity to permit assessment.
(i) Construct Δ ABC, in which BC = 8 cm, AB = 5 cm, ∠ ABC = 60°.
(ii) Construct the locus of point inside the triangle which are equidistant from BA and BC.
(iii) Construct the locus of points inside the triangle which are equidistant from B and C.
(iv) Mark as P, the point which is equidistant from AB, BC and also equidistant from B and C.
(v) Measure and record the length of PB.
Ruler and compasses only may be used in this question. All construction lines and arcs must be clearly shown, and be of sufficient length and clarity to permit assessment.
(i) Construct a ΔABC, in which BC = 6 cm, AB = 9 cm and ∠ABC = 60°.
(ii) Construct the locus of the vertices of the triangles with BC as base, which are equal in area to ΔABC.
(iii) Mark the point Q, in your construction, which would make ΔQBC equal in area to ΔABC, and isosceles.
(iv) Measure and record the length of CQ.
Given ∠BAC (Fig), determine the locus of a point which lies in the interior of ∠BAC and equidistant from two lines AB and AC.
ICSE solutions for Mathematics [English] Class 10 14 Loci (Locus and its Constructions) Graphical Depiction
Use graph paper for this question. Take 2 cm = 1 unit on both the axes.
- Plot the points A(1, 1), B(5, 3) and C(2, 7).
- Construct the locus of points equidistant from A and B.
- Construct the locus of points equidistant from AB and AC.
- Locate the point P such that PA = PB and P is equidistant from AB and AC.
- Measure and record the length PA in cm.
Solutions for 14: Loci (Locus and its Constructions)
![ICSE solutions for Mathematics [English] Class 10 chapter 14 - Loci (Locus and its Constructions) ICSE solutions for Mathematics [English] Class 10 chapter 14 - Loci (Locus and its Constructions) - Shaalaa.com](/images/mathematics-english-class-10_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
ICSE solutions for Mathematics [English] Class 10 chapter 14 - Loci (Locus and its Constructions)
Shaalaa.com has the CISCE Mathematics Mathematics [English] Class 10 CISCE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. ICSE solutions for Mathematics Mathematics [English] Class 10 CISCE 14 (Loci (Locus and its Constructions)) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. ICSE textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [English] Class 10 chapter 14 Loci (Locus and its Constructions) are Introduction of Loci, Loci Examples, Constructions Under Loci, Theorems Based on Loci.
Using ICSE Mathematics [English] Class 10 solutions Loci (Locus and its Constructions) exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in ICSE Solutions are essential questions that can be asked in the final exam. Maximum CISCE Mathematics [English] Class 10 students prefer ICSE Textbook Solutions to score more in exams.
Get the free view of Chapter 14, Loci (Locus and its Constructions) Mathematics [English] Class 10 additional questions for Mathematics Mathematics [English] Class 10 CISCE, and you can use Shaalaa.com to keep it handy for your exam preparation.
