Advertisements
Advertisements
प्रश्न
Given: ∠BAC, a line intersects the arms of ∠BAC in P and Q. How will you locate a point on line segment PQ, which is equidistant from AB and AC? Does such a point always exist?
Advertisements
उत्तर
Since, locus of points equidistant from AB and AC is the bisector of ∠BAC. Draw the bisector of ∠BAC intersecting PQ at R.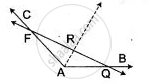
Since,R is on the bisector, so it is equidistant from AB and AC.
Yes, such a point always exists as there will be definitely a point where angular bisector and line will intersect.
Hence, R is the required point.
संबंधित प्रश्न
In each of the given figures; PA = PB and QA = QB.
| i. |  |
| ii. |  |
Prove, in each case, that PQ (produce, if required) is perpendicular bisector of AB. Hence, state the locus of the points equidistant from two given fixed points.
The given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F.
Prove that:
F is equidistant from A and B.
Draw an ∠ABC = 60°, having AB = 4.6 cm and BC = 5 cm. Find a point P equidistant from AB and BC; and also equidistant from A and B.
In the figure given below, find a point P on CD equidistant from points A and B.
Describe the locus of a runner, running around a circular track and always keeping a distance of 1.5 m from the inner edge.
Describe the locus of points at distances less than 3 cm from a given point.
Sketch and describe the locus of the vertices of all triangles with a given base and a given altitude.
Find the locus of points which are equidistant from three non-collinear points.
Show that the locus of the centres of all circles passing through two given points A and B, is the perpendicular bisector of the line segment AB.
Use ruler and compasses for the following question taking a scale of 10 m = 1 cm. A park in a city is bounded by straight fences AB, BC, CD and DA. Given that AB = 50 m, BC = 63 m, ∠ABC = 75°. D is a point equidistant from the fences AB and BC. If ∠BAD = 90°, construct the outline of the park ABCD. Also locate a point P on the line BD for the flag post which is equidistant from the corners of the park A and B.
