Advertisements
Advertisements
प्रश्न
In the given triangle ABC, find a point P equidistant from AB and AC; and also equidistant from B and C.
उत्तर
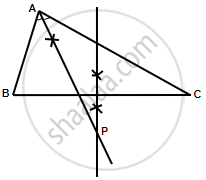
Steps of construction:
- In the given triangle, draw the angle bisector of ∠BAC.
- Draw the perpendicular bisector of BC which intersects the angle bisector at P.
P is the required point which is equidistant from AB and AC as well as from B and C.
Since P lies on angle bisector of ∠BAC,
It is equidistant from AB and AC.
Again, P lies on perpendicular bisector of BC,
Therefore, it is equidistant from B and C.
APPEARS IN
संबंधित प्रश्न
Construct a triangle ABC, in which AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm. Draw perpendicular bisector of BC which meets AC at point D. Prove that D is equidistant from B and C.
The given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F.
Prove that:
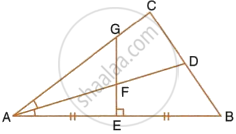
F is equidistant from AB and AC.
Describe the locus of the centre of a wheel of a bicycle going straight along a level road.
Describe the locus of the moving end of the minute hand of a clock.
Describe the locus of points inside a circle and equidistant from two fixed points on the circumference of the circle.
Describe the locus of points at distances less than 3 cm from a given point.
Describe the locus of points at distances greater than or equal to 35 mm from a given point.
In a quadrilateral ABCD, if the perpendicular bisectors of AB and AD meet at P, then prove that BP = DP.
Find the locus of points which are equidistant from three non-collinear points.
ΔPBC, ΔQBC and ΔRBC are three isosceles triangles on the same base BC. Show that P, Q and R are collinear.
