Advertisements
Advertisements
Question
In the given triangle ABC, find a point P equidistant from AB and AC; and also equidistant from B and C.
Solution
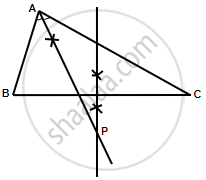
Steps of construction:
- In the given triangle, draw the angle bisector of ∠BAC.
- Draw the perpendicular bisector of BC which intersects the angle bisector at P.
P is the required point which is equidistant from AB and AC as well as from B and C.
Since P lies on angle bisector of ∠BAC,
It is equidistant from AB and AC.
Again, P lies on perpendicular bisector of BC,
Therefore, it is equidistant from B and C.
APPEARS IN
RELATED QUESTIONS
In each of the given figures; PA = PB and QA = QB.
| i. | 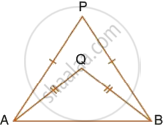 |
| ii. | 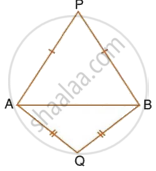 |
Prove, in each case, that PQ (produce, if required) is perpendicular bisector of AB. Hence, state the locus of the points equidistant from two given fixed points.
The given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F.
Prove that:
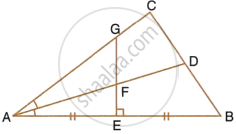
F is equidistant from A and B.
Draw an ∠ABC = 60°, having AB = 4.6 cm and BC = 5 cm. Find a point P equidistant from AB and BC; and also equidistant from A and B.
Describe the locus of points at a distance 2 cm from a fixed line.
Describe the locus of the centre of a wheel of a bicycle going straight along a level road.
Describe the locus of a point in rhombus ABCD, so that it is equidistant from
- AB and BC;
- B and D.
Describe the locus of points at distances greater than or equal to 35 mm from a given point.
Prove that the common chord of two intersecting circles is bisected at right angles by the line of centres.
Find the locus of points which are equidistant from three non-collinear points.
The bisectors of ∠B and ∠C of a quadrilateral ABCD intersect in P. Show that P is equidistant from the opposite sides AB and CD.
