Advertisements
Advertisements
Question
In each of the given figures; PA = PB and QA = QB.
| i. | 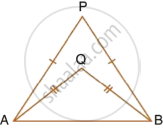 |
| ii. | 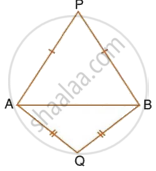 |
Prove, in each case, that PQ (produce, if required) is perpendicular bisector of AB. Hence, state the locus of the points equidistant from two given fixed points.
Solution
Construction: Join PQ which meets AB in D.
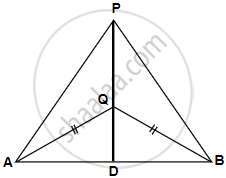
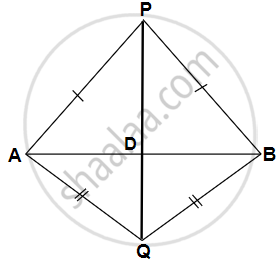
Proof: P is equidistant from A and B.
∴ P lies on the perpendicular bisector of AB.
Similarly, Q is equidistant from A and B.
∴ Q lies on perpendicular bisector of AB.
∴ P and Q both lie on the perpendicular bisector of AB.
∴ PQ is perpendicular bisector of AB.
Hence, locus of the points which are equidistant from two fixed points, is a perpendicular bisector of the line joining the fixed points.
APPEARS IN
RELATED QUESTIONS
In the given triangle ABC, find a point P equidistant from AB and AC; and also equidistant from B and C.
Construct a triangle ABC, with AB = 7 cm, BC = 8 cm and ∠ABC = 60°. Locate by construction the point P such that:
- P is equidistant from B and C.
- P is equidistant from AB and BC.
Measure and record the length of PB.
Describe the locus of the door handle, as the door opens.
Describe the locus of points at distances greater than 4 cm from a given point.
Sketch and describe the locus of the vertices of all triangles with a given base and a given altitude.
By actual drawing obtain the points equidistant from lines m and n; and 6 cm from a point P, where P is 2 cm above m, m is parallel to n and m is 6 cm above n.
A straight line AB is 8 cm long. Draw and describe the locus of a point which is:
- always 4 cm from the line AB.
- equidistant from A and B.
Mark the two points X and Y, which are 4 cm from AB and equidistant from A and B. Describe the figure AXBY.
Prove that the common chord of two intersecting circles is bisected at right angles by the line of centres.
The bisectors of ∠B and ∠C of a quadrilateral ABCD intersect in P. Show that P is equidistant from the opposite sides AB and CD.
Use ruler and compasses for the following question taking a scale of 10 m = 1 cm. A park in a city is bounded by straight fences AB, BC, CD and DA. Given that AB = 50 m, BC = 63 m, ∠ABC = 75°. D is a point equidistant from the fences AB and BC. If ∠BAD = 90°, construct the outline of the park ABCD. Also locate a point P on the line BD for the flag post which is equidistant from the corners of the park A and B.
