Advertisements
Advertisements
प्रश्न
In each of the given figures; PA = PB and QA = QB.
| i. | 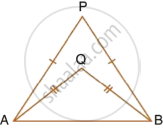 |
| ii. | 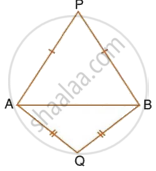 |
Prove, in each case, that PQ (produce, if required) is perpendicular bisector of AB. Hence, state the locus of the points equidistant from two given fixed points.
उत्तर
Construction: Join PQ which meets AB in D.
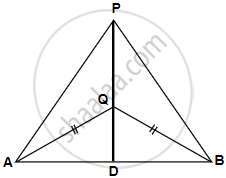
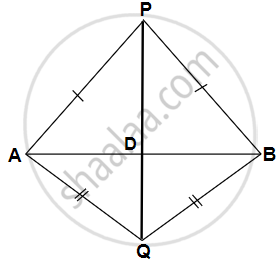
Proof: P is equidistant from A and B.
∴ P lies on the perpendicular bisector of AB.
Similarly, Q is equidistant from A and B.
∴ Q lies on perpendicular bisector of AB.
∴ P and Q both lie on the perpendicular bisector of AB.
∴ PQ is perpendicular bisector of AB.
Hence, locus of the points which are equidistant from two fixed points, is a perpendicular bisector of the line joining the fixed points.
APPEARS IN
संबंधित प्रश्न
Construct a triangle ABC, in which AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm. Draw perpendicular bisector of BC which meets AC at point D. Prove that D is equidistant from B and C.
The given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F.
Prove that:
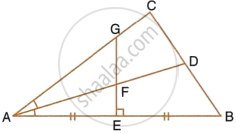
F is equidistant from A and B.
The given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F.
Prove that:
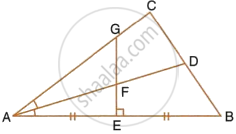
F is equidistant from AB and AC.
Construct a triangle ABC, with AB = 7 cm, BC = 8 cm and ∠ABC = 60°. Locate by construction the point P such that:
- P is equidistant from B and C.
- P is equidistant from AB and BC.
Measure and record the length of PB.
Describe the locus of points at a distance 2 cm from a fixed line.
Describe the locus of a stone dropped from the top of a tower.
In a quadrilateral PQRS, if the bisectors of ∠ SPQ and ∠ PQR meet at O, prove that O is equidistant from PS and QR.
In Fig. AB = AC, BD and CE are the bisectors of ∠ABC and ∠ACB respectively such that BD and CE intersect each other at O. AO produced meets BC at F. Prove that AF is the right bisector of BC.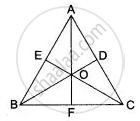
Given: ∠BAC, a line intersects the arms of ∠BAC in P and Q. How will you locate a point on line segment PQ, which is equidistant from AB and AC? Does such a point always exist?
Use ruler and compasses for the following question taking a scale of 10 m = 1 cm. A park in a city is bounded by straight fences AB, BC, CD and DA. Given that AB = 50 m, BC = 63 m, ∠ABC = 75°. D is a point equidistant from the fences AB and BC. If ∠BAD = 90°, construct the outline of the park ABCD. Also locate a point P on the line BD for the flag post which is equidistant from the corners of the park A and B.
