Advertisements
Advertisements
प्रश्न
Construct a right angled triangle PQR, in which ∠Q = 90°, hypotenuse PR = 8 cm and QR = 4.5 cm. Draw bisector of angle PQR and let it meets PR at point T. Prove that T is equidistant from PQ and QR.
उत्तर

Steps of Construction:
- Draw a line segment QR = 4.5 cm
- At Q, draw a ray QX making an angle of 90°
- With centre R and radius 8 cm, draw an arc which intersects QX at P.
- Join RP. ΔPQR is the required triangle.
- Draw the bisector of ∠PQR that meets PR in T.
- From T, draw perpendicular PL and PM respectively on PQ and QR.
Proof: In ΔLTQ and ΔMTQ
∠TLQ = ∠TMQ ...(Each = 90°)
∠LQT = ∠TQM ...(QT is angle bisector)
QT = QT ...(Common)
∴ By Angle – Angle – side criterion of congruence,
∴ ΔLTQ ≅ ΔMTQ ...(AAS postulate)
The corresponding parts of the congruent triangles are congruent
∴ TL = TM ...(C.P.C.T.)
Hence, T is equidistant from PQ and QR.
APPEARS IN
संबंधित प्रश्न
In each of the given figures; PA = PB and QA = QB.
| i. | 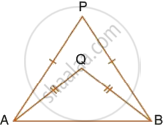 |
| ii. | 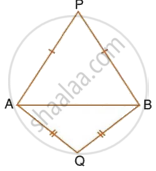 |
Prove, in each case, that PQ (produce, if required) is perpendicular bisector of AB. Hence, state the locus of the points equidistant from two given fixed points.
In the given triangle ABC, find a point P equidistant from AB and AC; and also equidistant from B and C.
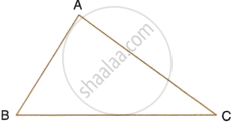
Describe the locus for questions 1 to 13 given below:
1. The locus of a point at a distant 3 cm from a fixed point.
Describe the locus of the centre of a wheel of a bicycle going straight along a level road.
Describe the locus of points inside a circle and equidistant from two fixed points on the circumference of the circle.
Describe the locus of points at distances less than 3 cm from a given point.
Prove that the common chord of two intersecting circles is bisected at right angles by the line of centres.
ΔPBC, ΔQBC and ΔRBC are three isosceles triangles on the same base BC. Show that P, Q and R are collinear.
In Fig. AB = AC, BD and CE are the bisectors of ∠ABC and ∠ACB respectively such that BD and CE intersect each other at O. AO produced meets BC at F. Prove that AF is the right bisector of BC.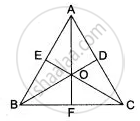
Given: ∠BAC, a line intersects the arms of ∠BAC in P and Q. How will you locate a point on line segment PQ, which is equidistant from AB and AC? Does such a point always exist?
