Advertisements
Advertisements
प्रश्न
In the given triangle ABC, find a point P equidistant from AB and AC; and also equidistant from B and C.
उत्तर
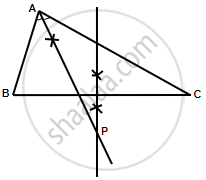
Steps of construction:
- In the given triangle, draw the angle bisector of ∠BAC.
- Draw the perpendicular bisector of BC which intersects the angle bisector at P.
P is the required point which is equidistant from AB and AC as well as from B and C.
Since P lies on angle bisector of ∠BAC,
It is equidistant from AB and AC.
Again, P lies on perpendicular bisector of BC,
Therefore, it is equidistant from B and C.
APPEARS IN
संबंधित प्रश्न
In parallelogram ABCD, side AB is greater than side BC and P is a point in AC such that PB bisects angle B. Prove that P is equidistant from AB and BC.
Draw a line AB = 6 cm. Draw the locus of all the points which are equidistant from A and B.
Draw an angle ABC = 75°. Draw the locus of all the points equidistant from AB and BC.
Draw an ∠ABC = 60°, having AB = 4.6 cm and BC = 5 cm. Find a point P equidistant from AB and BC; and also equidistant from A and B.
Describe the locus of points at a distance 2 cm from a fixed line.
Describe the locus of a stone dropped from the top of a tower.
Describe the locus of the door handle, as the door opens.
Describe the locus of points at distances greater than 4 cm from a given point.
In a quadrilateral ABCD, if the perpendicular bisectors of AB and AD meet at P, then prove that BP = DP.
Given: ∠BAC, a line intersects the arms of ∠BAC in P and Q. How will you locate a point on line segment PQ, which is equidistant from AB and AC? Does such a point always exist?
