Advertisements
Advertisements
प्रश्न
Describe the locus of points at a distance 2 cm from a fixed line.
उत्तर
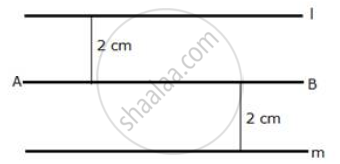
The locus of a point at a distance of 2 cm from a fixed line AB is a pair of straight lines l and m which are parallel to the given line at a distance of 2 cm.
APPEARS IN
संबंधित प्रश्न
Use ruler and compasses only for this question.
- Construct ΔABC, where AB = 3.5 cm, BC = 6 cm and ∠ABC = 60°.
- Construct the locus of points inside the triangle which are equidistant from BA and BC.
- Construct the locus of points inside the triangle which are equidistant from B and C.
- Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure and record the length of PB.
Construct a triangle ABC, with AB = 7 cm, BC = 8 cm and ∠ABC = 60°. Locate by construction the point P such that:
- P is equidistant from B and C.
- P is equidistant from AB and BC.
Measure and record the length of PB.
Describe the locus for questions 1 to 13 given below:
1. The locus of a point at a distant 3 cm from a fixed point.
Describe the locus of a runner, running around a circular track and always keeping a distance of 1.5 m from the inner edge.
The speed of sound is 332 metres per second. A gun is fired. Describe the locus of all the people on the earth’s surface, who hear the sound exactly one second later.
Sketch and describe the locus of the vertices of all triangles with a given base and a given altitude.
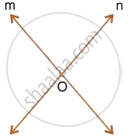
In the given figure, obtain all the points equidistant from lines m and n; and 2.5 cm from O.
A straight line AB is 8 cm long. Draw and describe the locus of a point which is:
- always 4 cm from the line AB.
- equidistant from A and B.
Mark the two points X and Y, which are 4 cm from AB and equidistant from A and B. Describe the figure AXBY.
In Δ ABC, the perpendicular bisector of AB and AC meet at 0. Prove that O is equidistant from the three vertices. Also, prove that if M is the mid-point of BC then OM meets BC at right angles.
Find the locus of points which are equidistant from three non-collinear points.
