Advertisements
Advertisements
प्रश्न
Use ruler and compasses only for this question.
- Construct ΔABC, where AB = 3.5 cm, BC = 6 cm and ∠ABC = 60°.
- Construct the locus of points inside the triangle which are equidistant from BA and BC.
- Construct the locus of points inside the triangle which are equidistant from B and C.
- Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure and record the length of PB.
उत्तर
Steps of construction:
- Draw line BC = 6 cm and an angle CBX = 60°. Cut off AB = 3.5. Join AC, triangle ABC is the required triangle.
- Draw perpendicular bisector of BC and bisector of angle B.
- Bisector of angle B meets bisector of BC at P.
`=>` BP is the required length, where, PB = 3.5 cm - P is the point which is equidistant from BA and BC, also equidistant from B and C.
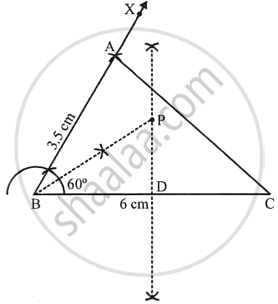
PB = 3.6 cm
APPEARS IN
संबंधित प्रश्न
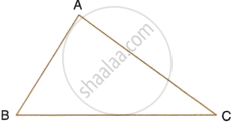
In the given triangle ABC, find a point P equidistant from AB and AC; and also equidistant from B and C.
Describe the locus of points at a distance 2 cm from a fixed line.
Describe the locus of the door handle, as the door opens.
Describe the locus of points at distances greater than 4 cm from a given point.
Describe the locus of points at distances greater than or equal to 35 mm from a given point.
In a quadrilateral PQRS, if the bisectors of ∠ SPQ and ∠ PQR meet at O, prove that O is equidistant from PS and QR.
In a quadrilateral ABCD, if the perpendicular bisectors of AB and AD meet at P, then prove that BP = DP.
ΔPBC, ΔQBC and ΔRBC are three isosceles triangles on the same base BC. Show that P, Q and R are collinear.
In Fig. AB = AC, BD and CE are the bisectors of ∠ABC and ∠ACB respectively such that BD and CE intersect each other at O. AO produced meets BC at F. Prove that AF is the right bisector of BC.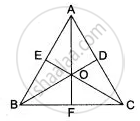
Use ruler and compasses for the following question taking a scale of 10 m = 1 cm. A park in a city is bounded by straight fences AB, BC, CD and DA. Given that AB = 50 m, BC = 63 m, ∠ABC = 75°. D is a point equidistant from the fences AB and BC. If ∠BAD = 90°, construct the outline of the park ABCD. Also locate a point P on the line BD for the flag post which is equidistant from the corners of the park A and B.
