Advertisements
Advertisements
प्रश्न
In Fig. AB = AC, BD and CE are the bisectors of ∠ABC and ∠ACB respectively such that BD and CE intersect each other at O. AO produced meets BC at F. Prove that AF is the right bisector of BC.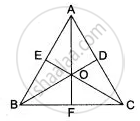
उत्तर
Given: A ΔABC in which AB = AC.
BD, the bisector of ∠ABC meets CE, the bisector of ∠ACB at O. AO produced meets BC at F.
To prove: AF is the right bisector of BC.
Proof: We have, AB = AC
⇒ A lies on the right bisector of BC ...(i)
and ∠ABC = ∠ACB
Now, ∠ABC = ∠ACB
⇒ `(1)/(2)`∠ABC = `(1)/(2)`∠ACB
⇒ ∠OBC = ∠OCB
[∵ BD and CE are bisector of ∠B and∠C respectively]
⇒ OB = OC
[∵ Sides opposite to equal angles are equal]
⇒ O lies on the right bisector of BC ...(iii)
From (i) and (ii), we obtain
⇒ A and O both lie on the right bisector of BC.
⇒ AO is the right bisector of BC
Hence, AF is the right bisector of BC.
Hence proved.
APPEARS IN
संबंधित प्रश्न
Construct a triangle ABC, in which AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm. Draw perpendicular bisector of BC which meets AC at point D. Prove that D is equidistant from B and C.
Construct a right angled triangle PQR, in which ∠Q = 90°, hypotenuse PR = 8 cm and QR = 4.5 cm. Draw bisector of angle PQR and let it meets PR at point T. Prove that T is equidistant from PQ and QR.
The given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F.
Prove that:
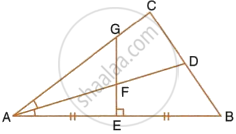
F is equidistant from AB and AC.
Draw a line AB = 6 cm. Draw the locus of all the points which are equidistant from A and B.
Draw an angle ABC = 75°. Draw the locus of all the points equidistant from AB and BC.
In the figure given below, find a point P on CD equidistant from points A and B.

Describe the locus of points at distances less than 3 cm from a given point.
Describe the locus of points at distances less than or equal to 2.5 cm from a given point.
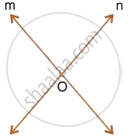
In the given figure, obtain all the points equidistant from lines m and n; and 2.5 cm from O.
ΔPBC, ΔQBC and ΔRBC are three isosceles triangles on the same base BC. Show that P, Q and R are collinear.
