Advertisements
Advertisements
Question
In Fig. AB = AC, BD and CE are the bisectors of ∠ABC and ∠ACB respectively such that BD and CE intersect each other at O. AO produced meets BC at F. Prove that AF is the right bisector of BC.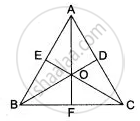
Advertisements
Solution
Given: A ΔABC in which AB = AC.
BD, the bisector of ∠ABC meets CE, the bisector of ∠ACB at O. AO produced meets BC at F.
To prove: AF is the right bisector of BC.
Proof: We have, AB = AC
⇒ A lies on the right bisector of BC ...(i)
and ∠ABC = ∠ACB
Now, ∠ABC = ∠ACB
⇒ `(1)/(2)`∠ABC = `(1)/(2)`∠ACB
⇒ ∠OBC = ∠OCB
[∵ BD and CE are bisector of ∠B and∠C respectively]
⇒ OB = OC
[∵ Sides opposite to equal angles are equal]
⇒ O lies on the right bisector of BC ...(iii)
From (i) and (ii), we obtain
⇒ A and O both lie on the right bisector of BC.
⇒ AO is the right bisector of BC
Hence, AF is the right bisector of BC.
Hence proved.
APPEARS IN
RELATED QUESTIONS
Construct a triangle ABC, in which AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm. Draw perpendicular bisector of BC which meets AC at point D. Prove that D is equidistant from B and C.
In triangle LMN, bisectors of interior angles at L and N intersect each other at point A. Prove that:
- Point A is equidistant from all the three sides of the triangle.
- AM bisects angle LMN.
Construct a triangle ABC, with AB = 7 cm, BC = 8 cm and ∠ABC = 60°. Locate by construction the point P such that:
- P is equidistant from B and C.
- P is equidistant from AB and BC.
- Measure and record the length of PB.
Describe the locus of points inside a circle and equidistant from two fixed points on the circumference of the circle.
In the given figure, obtain all the points equidistant from lines m and n; and 2.5 cm from O.
Draw a triangle ABC in which AB = 6 cm, BC = 4.5 cm and AC = 5 cm. Draw and label:
- the locus of the centres of all circles which touch AB and AC,
- the locus of the centres of all the circles of radius 2 cm which touch AB.
Hence, construct the circle of radius 2 cm which touches AB and AC .
In Δ ABC, the perpendicular bisector of AB and AC meet at 0. Prove that O is equidistant from the three vertices. Also, prove that if M is the mid-point of BC then OM meets BC at right angles.
In a quadrilateral ABCD, if the perpendicular bisectors of AB and AD meet at P, then prove that BP = DP.
ΔPBC and ΔQBC are two isosceles triangles on the same base. Show that the line PQ is bisector of BC and is perpendicular to BC.
ΔPBC, ΔQBC and ΔRBC are three isosceles triangles on the same base BC. Show that P, Q and R are collinear.
