Advertisements
Advertisements
Question
Show that the locus of the centres of all circles passing through two given points A and B, is the perpendicular bisector of the line segment AB.
Solution
Let P and Q be the centres of two circles S and S', each passing through two given points A and B. Then,
PA = PB ...[Radii of the same circle]
⇒ P lies on the perpendicular bisector of AB ...(i)
Again, QA = QB ...[Radii of the same circle]
⇒ Q lies on the perpendicular bisector of AB ...(ii)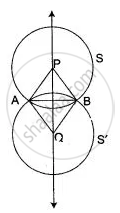
From (i) and (ii), it follows that P and Q both lies on the perpendicular bisector of AB.
Hence, the locus of the centres of all the circles passing through A and B is the perpendicular bisector of AB.
APPEARS IN
RELATED QUESTIONS
In triangle LMN, bisectors of interior angles at L and N intersect each other at point A. Prove that:
- Point A is equidistant from all the three sides of the triangle.
- AM bisects angle LMN.
The given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F.
Prove that:
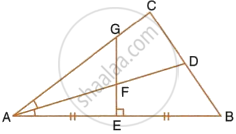
F is equidistant from AB and AC.
In the figure given below, find a point P on CD equidistant from points A and B.

Construct a triangle ABC, with AB = 7 cm, BC = 8 cm and ∠ABC = 60°. Locate by construction the point P such that:
- P is equidistant from B and C.
- P is equidistant from AB and BC.
Measure and record the length of PB.
Describe the locus of a point in rhombus ABCD, so that it is equidistant from
- AB and BC;
- B and D.
By actual drawing obtain the points equidistant from lines m and n; and 6 cm from a point P, where P is 2 cm above m, m is parallel to n and m is 6 cm above n.
In a quadrilateral PQRS, if the bisectors of ∠ SPQ and ∠ PQR meet at O, prove that O is equidistant from PS and QR.
Find the locus of the centre of a circle of radius r touching externally a circle of radius R.
ΔPBC, ΔQBC and ΔRBC are three isosceles triangles on the same base BC. Show that P, Q and R are collinear.
The bisectors of ∠B and ∠C of a quadrilateral ABCD intersect in P. Show that P is equidistant from the opposite sides AB and CD.
