Advertisements
Advertisements
Question
In a quadrilateral PQRS, if the bisectors of ∠ SPQ and ∠ PQR meet at O, prove that O is equidistant from PS and QR.
Solution

OP bisects ∠ SPQ and OQ bisects ∠ PQR.
Draw OM perpendirular to RQ and OL perpendirular to SP
Now in Δ OQM and Δ OLP
∠ OLP = ∠ OMQ
∠ OPL = ∠OQM
OP= OQ
Therefore, Δ OQM and Δ OLP are oongruent.
Hence, OL = OM
O is equidistant from PS and QR. Proved.
APPEARS IN
RELATED QUESTIONS
Construct a right angled triangle PQR, in which ∠Q = 90°, hypotenuse PR = 8 cm and QR = 4.5 cm. Draw bisector of angle PQR and let it meets PR at point T. Prove that T is equidistant from PQ and QR.
Draw an angle ABC = 75°. Draw the locus of all the points equidistant from AB and BC.
Draw an ∠ABC = 60°, having AB = 4.6 cm and BC = 5 cm. Find a point P equidistant from AB and BC; and also equidistant from A and B.
In the figure given below, find a point P on CD equidistant from points A and B.

Describe the locus of points at a distance 2 cm from a fixed line.
Describe the locus of the door handle, as the door opens.
Describe the locus of points at distances less than or equal to 2.5 cm from a given point.
Prove that the common chord of two intersecting circles is bisected at right angles by the line of centres.
In Fig. ABCD is a quadrilateral in which AB = BC. E is the point of intersection of the right bisectors of AD and CD. Prove that BE bisects ∠ABC.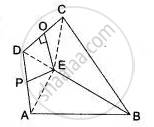
ΔPBC and ΔQBC are two isosceles triangles on the same base BC but on the opposite sides of line BC. Show that PQ bisects BC at right angles.
