Frank solutions for Mathematics - Part 2 [English] Class 10 ICSE chapter 16 - Loci [Latest edition]

Draw a straight line AB of 9 cm. Draw the locus of all points which are equidistant from A and B. Prove your statement. 

Two straight roads AB and CD cross each other at Pat an angle of 75°  . X is a stone on the road AB, 800m from P towards B. BY taking an appropriate scale draw a figure to locate the position of a pole, which is equidistant from P and X, and is also equidistant from the roads. 

Draw two intersecting lines to include an angle of 30°. Use ruler and compasses to locate points which are equidistant from these Iines and also 2 cm away from their point of intersection. How many such points exist? 

AB and CD are two intersecting lines. Find a point equidistant from AB and CD, and also at a distance of 1.8 cm from another given line EF. 

Without using set squares or protractor, construct a quadrilateral ABCD in which ∠ BAD = 45° , AD = AB = 6 cm, BC= 3.6 cm and CD=5 cm. Locate the point P on BD which is equidistant from BC and CD. 

Construct a rhombus ABCD with sides of length 5 cm and diagonal AC of length 6 cm. Measure ∠ ABC. Find the point R on AD such that RB = RC. Measure the length of AR. 

Construct a rhombus ABCD whose diagonals AC and BD are 8 cm and 6 cm respectively. Find by construction a point P equidistant from AB and AD and also from C and D. 

Construct a ti.PQR, in which PQ=S. 5 cm, QR=3. 2 cm and PR=4.8 cm. Draw the locus of a point which moves so that it is always 2.5 cm from Q. 

Construct a Δ XYZ in which XY= 4 cm, YZ = 5 cm and ∠ Y = 1200. Locate a point T such that ∠ YXT is a right angle and Tis equidistant from Y and Z. Measure TZ. 

In  Δ PQR, s is a point on PR such that ∠ PQS = ∠  RQS . Prove thats is equidistant from PQ and QR. 

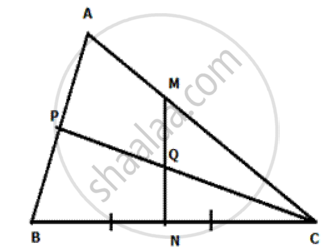
In the given figure ABC is a triangle. CP bisects angle ACB and MN is perpendicular bisector of BC. MN cuts CP at Q. Prove Q is equidistant from B and C, and also that Q is equidistant from BC and AC. 

A and B are fixed points while Pis a moving point, moving in a way that it is always equidistant from A and B. What is the locus of the path traced out by the pcint P? 

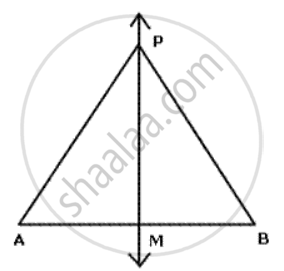
In given figure, ABCD is a kite. AB = AD and BC =CD. Prove that the diagona AC is the perpendirular bisector of the diagonal BD. 

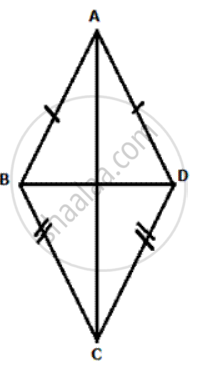
In given figure 1 ABCD is an arrowhead. AB = AD and BC = CD. Prove th at AC produced bisects BD at right angles at the point M

In Δ PQR, bisectors of  ∠ PQR and ∠ PRQ meet at I. Prove that I is equidistant from the three sides of the triangle , and PI bisects ∠ QPR . 

In  Δ ABC, the perpendicular bisector of AB and AC meet at 0. Prove that O is equidistant from the three vertices. Also, prove that if M is the mid-point of BC then OM meets BC at right angles. 

In a quadrilateral PQRS, if the bisectors of ∠ SPQ and ∠ PQR meet at O, prove that O is equidistant from PS and QR. 

In a quadrilateral ABCD, if the perpendicular bisectors of AB and AD meet at P, then prove that BP = DP. 

In Δ ABC, B and Care fixed points. Find the locus of point A which moves such that the area of Δ ABC remains the same. 

A point moves such that its distance from a fixed line AB is always the same. What is the relation between AB and the path travelled by the point? 

State the locus of a point moving so that its perpendicular distances from two given lines is always equal. 

AB is a fixed line) state the locus of the point P such that ∠ APB = 90° . 

Draw and describe the lorus in  the following cases: 

The locus of points at a distance of 4 cm from a fixed line. 

Draw and describe the lorus in the following cases: 

The lorus of points inside a circle and equidistant from two fixed points on the circle .

Draw and describe the lorus in the following cases: 

The Iocus of the mid-points of all parallel chords of a circle.

Draw and describe the lorus in the following cases: 

The lorus of a point in rhombus ABCD which is equidistant from AB and AD .

Draw and describe the locus in the following cases :

The locus of a point in the rhombus ABCD which is equidistant from the point  A and C

Describe completely the locus of point in  the following cases: 

Midpoint of radii of a circle. 

Describe completely the locus of point in the following cases: 

Centre of a ball, rolling along a straight line on a level floor. 

Describe completely the locus of points in the following cases: 

Point in a plane equidistant from a given line. 

Describe completely the locus of points in the following cases: 

Centre of a circle of varying radius and touching the two arms of ∠ ABC. 

Describe completely the locus of points in the following cases: 

Centre of a cirde of radius 2 cm and touching a fixed circle of radius 3 cm with centre O. 

Using only ruler and compasses, construct a triangle ABC 1 with AB = 5 cm, BC = 3.5 cm and AC= 4 cm. Mark a point P, which is equidistant from AB, BC and also from Band C. Measure the length of PB. 

Construct a triangle ABC, such that AB= 6 cm, BC= 7.3 cm and CA= 5.2 cm. Locate a point which is equidistant from A, B and C.