Advertisements
Advertisements
Question
Using only ruler and compasses, construct a triangle ABC 1 with AB = 5 cm, BC = 3.5 cm and AC= 4 cm. Mark a point P, which is equidistant from AB, BC and also from Band C. Measure the length of PB.
Solution
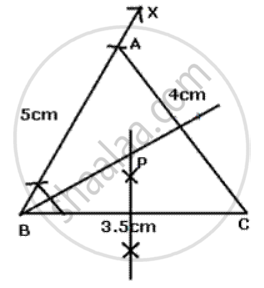
Steps of construction:
(i) Draw a line segment BC = 3. 5 cm.
(ii) With Bas centre and radius 5 cm draw an arc.
(iii) With C as centre and radius 4 cm draw another arc which intersects the first arc at A.
(iv) Join AB and AC.
(v) Dr aw perpendi cu I ar bi sector of BC.
(vi) Dr aw the angle bi sector of angle ABC which intersects the perpendicular bisector of BC at P.
Pis the required point which is equidistant from AB, BC, Band C.
The length of PB = 2.5 cm
APPEARS IN
RELATED QUESTIONS
Use ruler and compasses only for this question:
I. Construct ABC, where AB = 3.5 cm, BC = 6 cm and ABC = 60o.
II. Construct the locus of points inside the triangle which are equidistant from BA and BC.
III. Construct the locus of points inside the triangle which are equidistant from B and C.
IV. Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure and records the length of PB.
Use ruler and compasses only for this question. Draw a circle of radius 4 cm and mark two chords AB and AC of the circle of lengths 6 cm and 5 cm respectively.
(i) Construct the locus of points, inside the circle, that are equidistant from A and C. prove your construction.
(ii) Construct the locus of points, inside the circle that are equidistant from AB and AC.
Plot the points A(2, 9), B(–1, 3) and C(6, 3) on graph paper. On the same graph paper draw the locus of point A so that the area of ΔABC remains the same as A moves.
Draw two intersecting lines to include an angle of 30°. Use ruler and compasses to locate points which are equidistant from these Iines and also 2 cm away from their point of intersection. How many such points exist?
In the given figure ABC is a triangle. CP bisects angle ACB and MN is perpendicular bisector of BC. MN cuts CP at Q. Prove Q is equidistant from B and C, and also that Q is equidistant from BC and AC.
A and B are fixed points while Pis a moving point, moving in a way that it is always equidistant from A and B. What is the locus of the path traced out by the pcint P?
Construct a triangle ABC, such that AB= 6 cm, BC= 7.3 cm and CA= 5.2 cm. Locate a point which is equidistant from A, B and C.
State and draw the locus of a swimmer maintaining the same distance from a lighthouse.
Using a ruler and compass only:
(i) Construct a triangle ABC with BC = 6 cm, ∠ABC = 120° and AB = 3.5 cm.
(ii) In the above figure, draw a circle with BC as diameter. Find a point 'P' on the circumference of the circle which is equidistant from Ab and BC.
Measure ∠BCP.
Use ruler and compass to answer this question. Construct ∠ABC = 90°, where AB = 6 cm, BC = 8 cm.
- Construct the locus of points equidistant from B and C.
- Construct the locus of points equidistant from A and B.
- Mark the point which satisfies both the conditions (a) and (b) as 0. Construct the locus of points keeping a fixed distance OA from the fixed point 0.
- Construct the locus of points which are equidistant from BA and BC.
