Advertisements
Advertisements
Question
In the given figure ABC is a triangle. CP bisects angle ACB and MN is perpendicular bisector of BC. MN cuts CP at Q. Prove Q is equidistant from B and C, and also that Q is equidistant from BC and AC.
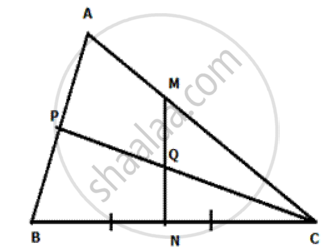
Solution
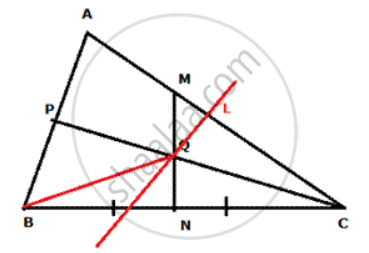
Join BQ and draw perpendicular bisector of AC cutting AC at L.
In Δ QBN and ΔQCN
QN = QN
BN =NC
∠ QNB = ∠ QNC = 90 degree.
Therefore, ∠ QBN and ∠.QCN are congruent .
Hence Q is equidistant from B and C.
In Δ QNC and Δ QLC
QC= QC
∠ QLC = ∠ QNC = 90 degree.
∠ QCL =∠ QCN (PC being angle bisector)
Therefore, .Δ QNC and Δ QLC are congruent.
Therefore, QL = QN.
Hence Q is equidistant from BC and AC.
APPEARS IN
RELATED QUESTIONS
Describe the locus of vertices of all isosceles triangles having a common base.
Construct a triangle ABC, with AB = 6 cm, AC = BC = 9 cm. Find a point 4 cm from A and equidistant from B and C.
Construct a rhombus ABCD whose diagonals AC and BD are 8 cm and 6 cm respectively. Find by construction a point P equidistant from AB and AD and also from C and D.
A and B are fixed points while Pis a moving point, moving in a way that it is always equidistant from A and B. What is the locus of the path traced out by the pcint P?
Describe completely the locus of point in the following cases:
Midpoint of radii of a circle.
Construct a triangle ABC, such that AB= 6 cm, BC= 7.3 cm and CA= 5.2 cm. Locate a point which is equidistant from A, B and C.
Use ruler and compass only for the following question. All construction lines and arcs must be clearly shown.
- Construct a ΔABC in which BC = 6.5 cm, ∠ABC = 60°, AB = 5 cm.
- Construct the locus of points at a distance of 3.5 cm from A.
- Construct the locus of points equidistant from AC and BC.
- Mark 2 points X and Y which are at a distance of 3.5 cm from A and also equidistant from AC and BC. Measure XY.
Construct a Δ ABC, with AB = 6 cm, AC = BC = 9 cm; find a point 4 cm from A and equidistant from B and C.
Using a ruler and compass only:
(i) Construct a triangle ABC with BC = 6 cm, ∠ABC = 120° and AB = 3.5 cm.
(ii) In the above figure, draw a circle with BC as diameter. Find a point 'P' on the circumference of the circle which is equidistant from Ab and BC.
Measure ∠BCP.
Use ruler and compasses only for the following questions:
Construct triangle BCP, when CB = 5 cm, BP = 4 cm, ∠PBC = 45°.
Complete the rectangle ABCD such that :
(i) P is equidistant from AB and BC and
(ii) P is equidistant from C and D. Measure and write down the length of AB.
