Advertisements
Advertisements
प्रश्न
In the given figure ABC is a triangle. CP bisects angle ACB and MN is perpendicular bisector of BC. MN cuts CP at Q. Prove Q is equidistant from B and C, and also that Q is equidistant from BC and AC.
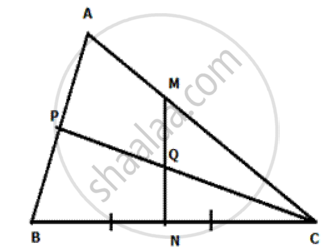
उत्तर
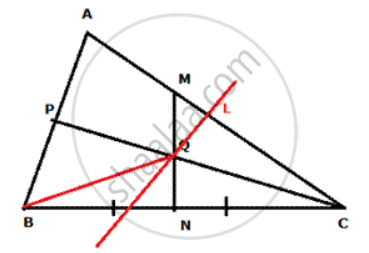
Join BQ and draw perpendicular bisector of AC cutting AC at L.
In Δ QBN and ΔQCN
QN = QN
BN =NC
∠ QNB = ∠ QNC = 90 degree.
Therefore, ∠ QBN and ∠.QCN are congruent .
Hence Q is equidistant from B and C.
In Δ QNC and Δ QLC
QC= QC
∠ QLC = ∠ QNC = 90 degree.
∠ QCL =∠ QCN (PC being angle bisector)
Therefore, .Δ QNC and Δ QLC are congruent.
Therefore, QL = QN.
Hence Q is equidistant from BC and AC.
APPEARS IN
संबंधित प्रश्न
Draw an angle ABC = 75°. Find a point P such that P is at a distance of 2 cm from AB and 1.5 cm from BC.
State the locus of a point in a rhombus ABCD, which is equidistant
- from AB and AD;
- from the vertices A and C.
Draw a straight line AB of 9 cm. Draw the locus of all points which are equidistant from A and B. Prove your statement.
AB and CD are two intersecting lines. Find a point equidistant from AB and CD, and also at a distance of 1.8 cm from another given line EF.
Construct a Δ XYZ in which XY= 4 cm, YZ = 5 cm and ∠ Y = 1200. Locate a point T such that ∠ YXT is a right angle and Tis equidistant from Y and Z. Measure TZ.
Describe completely the locus of points in the following cases:
Point in a plane equidistant from a given line.
Describe completely the locus of points in the following cases:
Centre of a circle of varying radius and touching the two arms of ∠ ABC.
Draw and describe the locus in the following cases :
The locus of a point in the rhombus ABCD which is equidistant from the point A and C
Construct a triangle BPC given BC = 5 cm, BP = 4 cm and .
i) complete the rectangle ABCD such that:
a) P is equidistant from AB and BCV
b) P is equidistant from C and D.
ii) Measure and record the length of AB.
Without using set squares or protractor construct:
(i) Triangle ABC, in which AB = 5.5 cm, BC = 3.2 cm and CA = 4.8 cm.
(ii) Draw the locus of a point which moves so that it is always 2.5 cm from B.
(iii) Draw the locus of a point which moves so that it is equidistant from the sides BC and CA.
(iv) Mark the point of intersection of the loci with the letter P and measure PC.
