Advertisements
Advertisements
प्रश्न
Draw a straight line AB of 9 cm. Draw the locus of all points which are equidistant from A and B. Prove your statement.
उत्तर
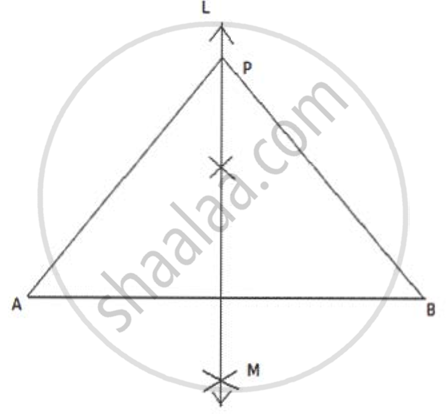
Steps of oonstruction:
(i) Draw a line segment AB of 9 cm.
(ii) Draw perpendicular bisector LM of AB. LM is the required locus.
Proof:
(i) Take any point on LM say P.
(ii) Join PA and PB.
Since, Plies on the right bisector of line AB.
Therefore, Pis equidistant from A and B.
i.e. PA = PB
Hence, Perpendicular bisector of AB is the locus of all points which are equidistant from A and B.
APPEARS IN
संबंधित प्रश्न
Describe the locus of vertices of all isosceles triangles having a common base.
Draw an angle ABC = 75°. Find a point P such that P is at a distance of 2 cm from AB and 1.5 cm from BC.
Two straight roads AB and CD cross each other at Pat an angle of 75° . X is a stone on the road AB, 800m from P towards B. BY taking an appropriate scale draw a figure to locate the position of a pole, which is equidistant from P and X, and is also equidistant from the roads.
AB and CD are two intersecting lines. Find a point equidistant from AB and CD, and also at a distance of 1.8 cm from another given line EF.
In Δ PQR, bisectors of ∠ PQR and ∠ PRQ meet at I. Prove that I is equidistant from the three sides of the triangle , and PI bisects ∠ QPR .
Draw and describe the lorus in the following cases:
The locus of points at a distance of 4 cm from a fixed line.
Draw and describe the lorus in the following cases:
The lorus of a point in rhombus ABCD which is equidistant from AB and AD .
Construct a triangle BPC given BC = 5 cm, BP = 4 cm and .
i) complete the rectangle ABCD such that:
a) P is equidistant from AB and BCV
b) P is equidistant from C and D.
ii) Measure and record the length of AB.
Construct a Δ ABC, with AB = 6 cm, AC = BC = 9 cm; find a point 4 cm from A and equidistant from B and C.
How will you find a point equidistant from three given points A, B, C which are not in the same straight line?
