Advertisements
Advertisements
प्रश्न
Two straight roads AB and CD cross each other at Pat an angle of 75° . X is a stone on the road AB, 800m from P towards B. BY taking an appropriate scale draw a figure to locate the position of a pole, which is equidistant from P and X, and is also equidistant from the roads.
उत्तर
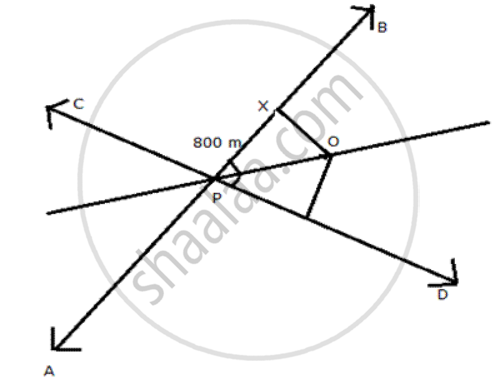
Steps of construction:
(i) Draw two lines AB and CD crossing at an angle of 75 °
(ii) Draw an angle bisector for ∠ BPD
(iii) Draw perpendicular from X on angle bisector meeting at 0.
(iv) From point Y, PX = PY, draw a perpendicular on angle bisector meeting at 0.
(v) 0 is the point which is equidistant from P, X and both the roads.
cos θ = `"hypotenuse"/"base"`
cos `75/2 = "PO"/"PX"`
cos (37.5) = `"PO"/800`
0.980243 = `"PO"/800`
PO = 784.19 m
APPEARS IN
संबंधित प्रश्न
Describe the locus of vertices of all isosceles triangles having a common base.
Ruler and compasses may be used in this question. All construction lines and arcs must be clearly shown and be of sufficient length and clarity to permit assessment.
- Construct a ΔABC, in which BC = 6 cm, AB = 9 cm and angle ABC = 60°.
- Construct the locus of all points inside triangle ABC, which are equidistant from B and C.
- Construct the locus of the vertices of the triangles with BC as base and which are equal in area to triangle ABC.
- Mark the point Q, in your construction, which would make ΔQBC equal in area to ΔABC, and isosceles.
- Measure and record the length of CQ.
Draw a straight line AB of 9 cm. Draw the locus of all points which are equidistant from A and B. Prove your statement.
In Δ PQR, s is a point on PR such that ∠ PQS = ∠ RQS . Prove thats is equidistant from PQ and QR.
In given figure 1 ABCD is an arrowhead. AB = AD and BC = CD. Prove th at AC produced bisects BD at right angles at the point M

Draw and describe the lorus in the following cases:
The locus of points at a distance of 4 cm from a fixed line.
Describe completely the locus of point in the following cases:
Midpoint of radii of a circle.
Describe completely the locus of points in the following cases:
Point in a plane equidistant from a given line.
Use ruler and compass only for the following question. All construction lines and arcs must be clearly shown.
- Construct a ΔABC in which BC = 6.5 cm, ∠ABC = 60°, AB = 5 cm.
- Construct the locus of points at a distance of 3.5 cm from A.
- Construct the locus of points equidistant from AC and BC.
- Mark 2 points X and Y which are at a distance of 3.5 cm from A and also equidistant from AC and BC. Measure XY.
Use ruler and compasses only for the following questions:
Construct triangle BCP, when CB = 5 cm, BP = 4 cm, ∠PBC = 45°.
Complete the rectangle ABCD such that :
(i) P is equidistant from AB and BC and
(ii) P is equidistant from C and D. Measure and write down the length of AB.
