Advertisements
Advertisements
प्रश्न
Describe the locus of vertices of all isosceles triangles having a common base.
उत्तर
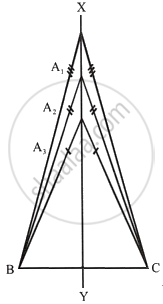
The locus of vertices of all isosceles triangles having a common base will be the perpendicular bisector of the common base of the triangles.
APPEARS IN
संबंधित प्रश्न
Draw an angle ABC = 75°. Find a point P such that P is at a distance of 2 cm from AB and 1.5 cm from BC.
Construct a rhombus ABCD whose diagonals AC and BD are 8 cm and 6 cm respectively. Find by construction a point P equidistant from AB and AD and also from C and D.
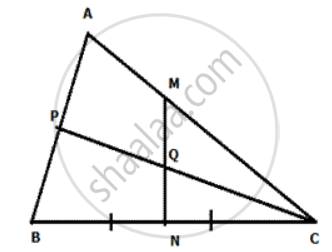
In the given figure ABC is a triangle. CP bisects angle ACB and MN is perpendicular bisector of BC. MN cuts CP at Q. Prove Q is equidistant from B and C, and also that Q is equidistant from BC and AC.
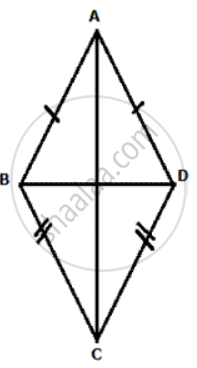
In given figure, ABCD is a kite. AB = AD and BC =CD. Prove that the diagona AC is the perpendirular bisector of the diagonal BD.
Draw and describe the lorus in the following cases:
The locus of points at a distance of 4 cm from a fixed line.
Draw and describe the lorus in the following cases:
The lorus of points inside a circle and equidistant from two fixed points on the circle .
State and draw the locus of a swimmer maintaining the same distance from a lighthouse.
Without using set squares or protractor.
(i) Construct a ΔABC, given BC = 4 cm, angle B = 75° and CA = 6 cm.
(ii) Find the point P such that PB = PC and P is equidistant from the side BC and BA. Measure AP.
Ruler and compasses only may be used in this question. All construction lines and arcs must be clearly shown, and be of sufficient length and clarity to permit assessment.
(i) Construct a ΔABC, in which BC = 6 cm, AB = 9 cm and ∠ABC = 60°.
(ii) Construct the locus of the vertices of the triangles with BC as base, which are equal in area to ΔABC.
(iii) Mark the point Q, in your construction, which would make ΔQBC equal in area to ΔABC, and isosceles.
(iv) Measure and record the length of CQ.
Use ruler and compass to answer this question. Construct ∠ABC = 90°, where AB = 6 cm, BC = 8 cm.
- Construct the locus of points equidistant from B and C.
- Construct the locus of points equidistant from A and B.
- Mark the point which satisfies both the conditions (a) and (b) as 0. Construct the locus of points keeping a fixed distance OA from the fixed point 0.
- Construct the locus of points which are equidistant from BA and BC.
