Advertisements
Advertisements
प्रश्न
Describe the locus of vertices of all isosceles triangles having a common base.
उत्तर
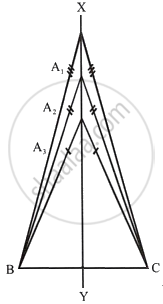
The locus of vertices of all isosceles triangles having a common base will be the perpendicular bisector of the common base of the triangles.
APPEARS IN
संबंधित प्रश्न
Construct a triangle ABC with AB = 5.5 cm, AC = 6 cm and ∠BAC = 105°
Hence:
1) Construct the locus of points equidistant from BA and BC
2) Construct the locus of points equidistant from B and C.
3) Mark the point which satisfies the above two loci as P. Measure and write the length of PC.
Angle ABC = 60° and BA = BC = 8 cm. The mid-points of BA and BC are M and N respectively. Draw and describe the locus of a point which is:
- equidistant from BA and BC.
- 4 cm from M.
- 4 cm from N.
Mark the point P, which is 4 cm from both M and N, and equidistant from BA and BC. Join MP and NP, and describe the figure BMPN.
Construct a triangle ABC, with AB = 5.6 cm, AC = BC = 9.2 cm. Find the points equidistant from AB and AC; and also 2 cm from BC. Measure the distance between the two points obtained.
Use graph paper for this question. Take 2 cm = 1 unit on both the axes.
- Plot the points A(1, 1), B(5, 3) and C(2, 7).
- Construct the locus of points equidistant from A and B.
- Construct the locus of points equidistant from AB and AC.
- Locate the point P such that PA = PB and P is equidistant from AB and AC.
- Measure and record the length PA in cm.
Construct a Δ XYZ in which XY= 4 cm, YZ = 5 cm and ∠ Y = 1200. Locate a point T such that ∠ YXT is a right angle and Tis equidistant from Y and Z. Measure TZ.
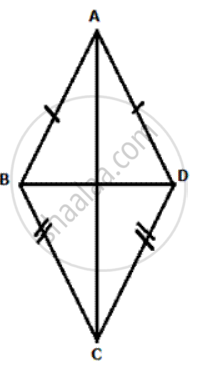
In given figure, ABCD is a kite. AB = AD and BC =CD. Prove that the diagona AC is the perpendirular bisector of the diagonal BD.
Draw and describe the lorus in the following cases:
The locus of points at a distance of 4 cm from a fixed line.
Draw and describe the lorus in the following cases:
The lorus of points inside a circle and equidistant from two fixed points on the circle .
State and draw the locus of a swimmer maintaining the same distance from a lighthouse.
Using only a ruler and compass construct ∠ABC = 120°, where AB = BC = 5 cm.
(i) Mark two points D and E which satisfy the condition that they are equidistant from both ABA and BC.
(ii) In the above figure, join AD, DC, AE and EC. Describe the figures:
(a) AECB, (b) ABD, (c) ABE.
