Advertisements
Advertisements
प्रश्न
Angle ABC = 60° and BA = BC = 8 cm. The mid-points of BA and BC are M and N respectively. Draw and describe the locus of a point which is:
- equidistant from BA and BC.
- 4 cm from M.
- 4 cm from N.
Mark the point P, which is 4 cm from both M and N, and equidistant from BA and BC. Join MP and NP, and describe the figure BMPN.
उत्तर
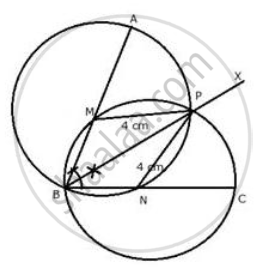
- Draw an angle of 60° with AB = BC = 8 cm
- Draw the angle bisector BX of ∠ABC
- With centre M and N, draw circles of radius equal to 4 cm, which intersects each other at P. P is the required point.
- Join MP, NP
BMPN is a rhombus since MP = BM = NB = NP = 4 cm
APPEARS IN
संबंधित प्रश्न
Use ruler and compasses only for this question:
I. Construct ABC, where AB = 3.5 cm, BC = 6 cm and ABC = 60o.
II. Construct the locus of points inside the triangle which are equidistant from BA and BC.
III. Construct the locus of points inside the triangle which are equidistant from B and C.
IV. Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure and records the length of PB.
On a graph paper, draw the line x = 6. Now, on the same graph paper, draw the locus of the point which moves in such a way that its distantce from the given line is always equal to 3 units
Describe the locus of vertices of all isosceles triangles having a common base.
Construct a ti.PQR, in which PQ=S. 5 cm, QR=3. 2 cm and PR=4.8 cm. Draw the locus of a point which moves so that it is always 2.5 cm from Q.
In given figure 1 ABCD is an arrowhead. AB = AD and BC = CD. Prove th at AC produced bisects BD at right angles at the point M

Draw and describe the lorus in the following cases:
The lorus of a point in rhombus ABCD which is equidistant from AB and AD .
Describe completely the locus of point in the following cases:
Centre of a ball, rolling along a straight line on a level floor.
State and draw the locus of a point equidistant from two given parallel lines.
Without using set squares or protractor construct:
(i) Triangle ABC, in which AB = 5.5 cm, BC = 3.2 cm and CA = 4.8 cm.
(ii) Draw the locus of a point which moves so that it is always 2.5 cm from B.
(iii) Draw the locus of a point which moves so that it is equidistant from the sides BC and CA.
(iv) Mark the point of intersection of the loci with the letter P and measure PC.
Given ∠BAC (Fig), determine the locus of a point which lies in the interior of ∠BAC and equidistant from two lines AB and AC.
