Advertisements
Advertisements
प्रश्न
Draw a triangle ABC in which AB = 6 cm, BC = 4.5 cm and AC = 5 cm. Draw and label:
- the locus of the centres of all circles which touch AB and AC,
- the locus of the centres of all the circles of radius 2 cm which touch AB.
Hence, construct the circle of radius 2 cm which touches AB and AC .
उत्तर
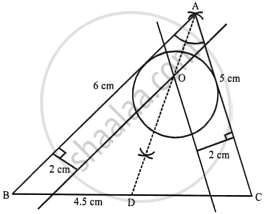
Steps of construction:
- Draw a line segment BC = 4.5 cm
- With B as centre and radius 6 cm and C as centre and radius 5 cm, draw arcs which intersect each other at A.
- Join AB and AC.
ABC is the required triangle. - Draw the angle bisector of ∠BAC
- Draw lines parallel to AB and AC at a distance of 2 cm, which intersect each other and AD at O.
- With centre O and radius 2 cm, draw a circle which touches AB and AC.
APPEARS IN
संबंधित प्रश्न
In each of the given figures; PA = PB and QA = QB.
| i. | 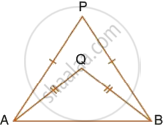 |
| ii. | 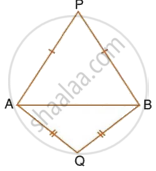 |
Prove, in each case, that PQ (produce, if required) is perpendicular bisector of AB. Hence, state the locus of the points equidistant from two given fixed points.
Use ruler and compasses only for this question.
- Construct ΔABC, where AB = 3.5 cm, BC = 6 cm and ∠ABC = 60°.
- Construct the locus of points inside the triangle which are equidistant from BA and BC.
- Construct the locus of points inside the triangle which are equidistant from B and C.
- Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure and record the length of PB.
In the given triangle ABC, find a point P equidistant from AB and AC; and also equidistant from B and C.
Construct a triangle ABC, with AB = 7 cm, BC = 8 cm and ∠ABC = 60°. Locate by construction the point P such that:
- P is equidistant from B and C.
- P is equidistant from AB and BC.
Measure and record the length of PB.
Describe the locus of the centres of all circles passing through two fixed points.
Describe the locus of a point in rhombus ABCD, so that it is equidistant from
- AB and BC;
- B and D.
The speed of sound is 332 metres per second. A gun is fired. Describe the locus of all the people on the earth’s surface, who hear the sound exactly one second later.
Describe the locus of points at distances greater than 4 cm from a given point.
Describe the locus of points at distances less than or equal to 2.5 cm from a given point.
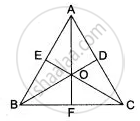
In Fig. AB = AC, BD and CE are the bisectors of ∠ABC and ∠ACB respectively such that BD and CE intersect each other at O. AO produced meets BC at F. Prove that AF is the right bisector of BC.