Advertisements
Advertisements
Question
Draw a triangle ABC in which AB = 6 cm, BC = 4.5 cm and AC = 5 cm. Draw and label:
- the locus of the centres of all circles which touch AB and AC,
- the locus of the centres of all the circles of radius 2 cm which touch AB.
Hence, construct the circle of radius 2 cm which touches AB and AC .
Solution
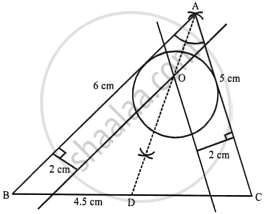
Steps of construction:
- Draw a line segment BC = 4.5 cm
- With B as centre and radius 6 cm and C as centre and radius 5 cm, draw arcs which intersect each other at A.
- Join AB and AC.
ABC is the required triangle. - Draw the angle bisector of ∠BAC
- Draw lines parallel to AB and AC at a distance of 2 cm, which intersect each other and AD at O.
- With centre O and radius 2 cm, draw a circle which touches AB and AC.
APPEARS IN
RELATED QUESTIONS
Construct a triangle ABC, in which AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm. Draw perpendicular bisector of BC which meets AC at point D. Prove that D is equidistant from B and C.
In triangle LMN, bisectors of interior angles at L and N intersect each other at point A. Prove that:
- Point A is equidistant from all the three sides of the triangle.
- AM bisects angle LMN.
Draw an ∠ABC = 60°, having AB = 4.6 cm and BC = 5 cm. Find a point P equidistant from AB and BC; and also equidistant from A and B.
In the figure given below, find a point P on CD equidistant from points A and B.

In the given triangle ABC, find a point P equidistant from AB and AC; and also equidistant from B and C.
Describe the locus of points at a distance 2 cm from a fixed line.
Describe the locus of a runner, running around a circular track and always keeping a distance of 1.5 m from the inner edge.
Describe the locus of points at distances greater than 4 cm from a given point.
A straight line AB is 8 cm long. Draw and describe the locus of a point which is:
- always 4 cm from the line AB.
- equidistant from A and B.
Mark the two points X and Y, which are 4 cm from AB and equidistant from A and B. Describe the figure AXBY.
Use ruler and compasses for the following question taking a scale of 10 m = 1 cm. A park in a city is bounded by straight fences AB, BC, CD and DA. Given that AB = 50 m, BC = 63 m, ∠ABC = 75°. D is a point equidistant from the fences AB and BC. If ∠BAD = 90°, construct the outline of the park ABCD. Also locate a point P on the line BD for the flag post which is equidistant from the corners of the park A and B.
