Advertisements
Advertisements
Question
Construct a triangle ABC, in which AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm. Draw perpendicular bisector of BC which meets AC at point D. Prove that D is equidistant from B and C.
Solution
Given: In triangle ABC, AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm
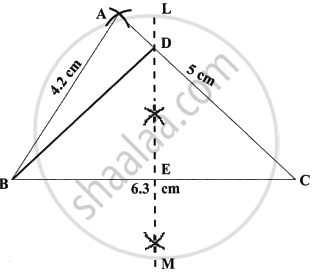
Steps of Construction:
- Draw a line segment BC = 6.3 cm
- With centre B and radius 4.2 cm, draw an arc.
- With centre C and radius 5 cm, draw another arc which intersects the first arc at A.
- Join AB and AC. ΔABC is the required triangle.
- Again with centre B and C and radius greater than 12 BC, draw arcs which intersects each other at L and M.
- Join LM intersecting AC at D and BC at E.
- Join DB.
Proof: In ΔDBE and ΔDCE
BE = EC ...(LM is bisector of BC)
∠DEB = ∠DEC ...(Each = 90°)
DE = DE ...(Common)
∴ By side angle side criterion of congruence, we have
ΔDBE ≅ ΔDCE ...(SAS postulate)
The corresponding parts of the congruent triangle are congruent
∴ DB = DC ...(C.P.C.T.)
Hence, D is equidistant from B and C.
APPEARS IN
RELATED QUESTIONS
In triangle LMN, bisectors of interior angles at L and N intersect each other at point A. Prove that:
- Point A is equidistant from all the three sides of the triangle.
- AM bisects angle LMN.
Draw an ∠ABC = 60°, having AB = 4.6 cm and BC = 5 cm. Find a point P equidistant from AB and BC; and also equidistant from A and B.
Construct a triangle ABC, with AB = 7 cm, BC = 8 cm and ∠ABC = 60°. Locate by construction the point P such that:
- P is equidistant from B and C.
- P is equidistant from AB and BC.
Measure and record the length of PB.
Describe the locus of points at a distance 2 cm from a fixed line.
Describe the locus of the centres of all circles passing through two fixed points.
Describe the locus of points at distances greater than 4 cm from a given point.
In a quadrilateral PQRS, if the bisectors of ∠ SPQ and ∠ PQR meet at O, prove that O is equidistant from PS and QR.
Prove that the common chord of two intersecting circles is bisected at right angles by the line of centres.
ΔPBC and ΔQBC are two isosceles triangles on the same base. Show that the line PQ is bisector of BC and is perpendicular to BC.
In Fig. AB = AC, BD and CE are the bisectors of ∠ABC and ∠ACB respectively such that BD and CE intersect each other at O. AO produced meets BC at F. Prove that AF is the right bisector of BC.