Advertisements
Advertisements
Question
Given: AX bisects angle BAC and PQ is perpendicular bisector of AC which meets AX at point Y.
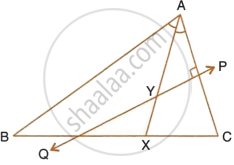
Prove:
- X is equidistant from AB and AC.
- Y is equidistant from A and C.
Solution
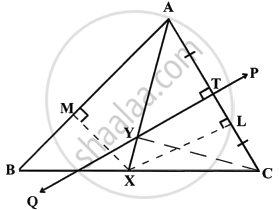
Construction: From X, draw XL ⊥ AC and XM ⊥ AB. Also join YC.
Proof:
i. In ΔAXL and ΔAXM,
∠XAL = ∠XAM ...(Given)
AX = AX ...(Common)
∠XLA = ∠XMA ...(Each = 90°)
∴ By Angle side angle criterion of congruence,
ΔAXL ≅ ΔAXM ...(ASA Postulate)
The corresponding parts of the congruent triangles are congruent
∴ XL = XM ...(C.P.C.T.)
Hence, X is equidistant from AB and AC
ii. In ΔYTA and ΔYTC,
AT = CT ...(∵ PQ is a perpendicular bisector of AC)
∠YTA = ∠YTC ...(Each = 90°)
YT = YT ...(Common)
∴ By side – Angle – side criterion of congruence,
∴ ΔYTA ≅ ΔYTC ...(SAS postulate)
The corresponding parts of the congruent triangle are congruent.
∴ YA = YC ...(C.P.C.T.)
Hence, Y is equidistant from A and C.
APPEARS IN
RELATED QUESTIONS
Given: PQ is perpendicular bisector of side AB of the triangle ABC.
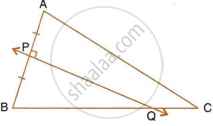
Prove: Q is equidistant from A and B.
Given: CP is bisector of angle C of ΔABC.
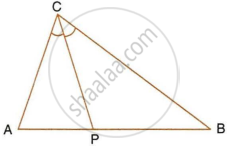
Prove: P is equidistant from AC and BC.
Construct a triangle ABC in which angle ABC = 75°, AB = 5 cm and BC = 6.4 cm. Draw perpendicular bisector of side BC and also the bisector of angle ACB. If these bisectors intersect each other at point P; prove that P is equidistant from B and C; and also from AC and BC.
Describe the locus of the centre of a given circle which rolls around the outside of a second circle and is always touching it.
Describe the locus of the centres of all circles that are tangent to both the arms of a given angle.
Describe the locus of the mid-points of all chords parallel to a given chord of a circle.
Describe the locus of points within a circle that are equidistant from the end points of a given chord.
Construct a triangle ABC, having given AB = 4.8 cm, AC = 4 cm, and ∠A = 75°. Find a point P.
- inside the triangle ABC.
- outside the triangle ABC
Equidistant from B and C; and at a distance of 1.2 cm from BC.
