Advertisements
Advertisements
Question
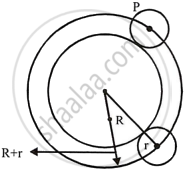
Describe the locus of the centre of a given circle which rolls around the outside of a second circle and is always touching it.
Solution
The locus is the circumference of the circle concentric with the second circle whose radius is equal to the sum of the radii of the two given circles.
APPEARS IN
RELATED QUESTIONS
Given: PQ is perpendicular bisector of side AB of the triangle ABC.
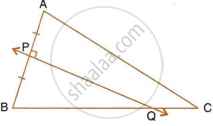
Prove: Q is equidistant from A and B.
Given: CP is bisector of angle C of ΔABC.
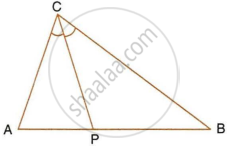
Prove: P is equidistant from AC and BC.
Given: AX bisects angle BAC and PQ is perpendicular bisector of AC which meets AX at point Y.
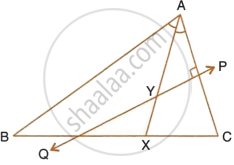
Prove:
- X is equidistant from AB and AC.
- Y is equidistant from A and C.
Construct a triangle ABC in which angle ABC = 75°, AB = 5 cm and BC = 6.4 cm. Draw perpendicular bisector of side BC and also the bisector of angle ACB. If these bisectors intersect each other at point P; prove that P is equidistant from B and C; and also from AC and BC.
Describe the locus of the centres of all circles that are tangent to both the arms of a given angle.
Describe the locus of the mid-points of all chords parallel to a given chord of a circle.
Describe the locus of points within a circle that are equidistant from the end points of a given chord.
Construct a triangle ABC, having given AB = 4.8 cm, AC = 4 cm, and ∠A = 75°. Find a point P.
- inside the triangle ABC.
- outside the triangle ABC
Equidistant from B and C; and at a distance of 1.2 cm from BC.
