Advertisements
Advertisements
प्रश्न
State and draw the locus of a point equidistant from two given parallel lines.
उत्तर

The locus of a point equidistant from two given parallel lines AB and CD is the line EF parallel to AB or CD exactly mid-way between AB and CD.
APPEARS IN
संबंधित प्रश्न
On a graph paper, draw the line x = 6. Now, on the same graph paper, draw the locus of the point which moves in such a way that its distantce from the given line is always equal to 3 units
Describe the locus of a point P, so that:
AB2 = AP2 + BP2,
where A and B are two fixed points.
O is a fixed point. Point P moves along a fixed line AB. Q is a point on OP produced such that OP = PQ. Prove that the locus of point Q is a line parallel to AB.
Construct an isosceles triangle ABC such that AB = 6 cm, BC = AC = 4 cm. Bisect ∠C internally and mark a point P on this bisector such that CP = 5 cm. Find the points Q and R which are 5 cm from P and also 5 cm from the line AB.
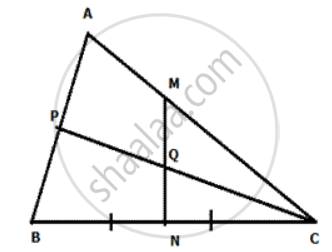
In the given figure ABC is a triangle. CP bisects angle ACB and MN is perpendicular bisector of BC. MN cuts CP at Q. Prove Q is equidistant from B and C, and also that Q is equidistant from BC and AC.
Describe completely the locus of points in the following cases:
Point in a plane equidistant from a given line.
Describe completely the locus of points in the following cases:
Centre of a circle of varying radius and touching the two arms of ∠ ABC.
Describe completely the locus of points in the following cases:
Centre of a cirde of radius 2 cm and touching a fixed circle of radius 3 cm with centre O.
Construct a triangle ABC, such that AB= 6 cm, BC= 7.3 cm and CA= 5.2 cm. Locate a point which is equidistant from A, B and C.
Using ruler and compasses construct:
(i) a triangle ABC in which AB = 5.5 cm, BC = 3.4 cm and CA = 4.9 cm.
(ii) the locus of point equidistant from A and C.
(iii) a circle touching AB at A and passing through C.
