Advertisements
Advertisements
प्रश्न
Describe the locus of a point P, so that:
AB2 = AP2 + BP2,
where A and B are two fixed points.
उत्तर
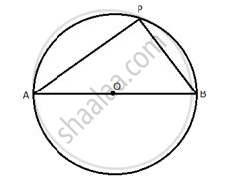
The locus of the point P is the circumference of a circle with AB as diameter and satisfies the condition AB2 = AP2 + BP2
APPEARS IN
संबंधित प्रश्न
Construct an isosceles triangle ABC such that AB = 6 cm, BC = AC = 4 cm. Bisect ∠C internally and mark a point P on this bisector such that CP = 5 cm. Find the points Q and R which are 5 cm from P and also 5 cm from the line AB.
Plot the points A(2, 9), B(–1, 3) and C(6, 3) on graph paper. On the same graph paper draw the locus of point A so that the area of ΔABC remains the same as A moves.
Draw a straight line AB of 9 cm. Draw the locus of all points which are equidistant from A and B. Prove your statement.
Construct a rhombus ABCD with sides of length 5 cm and diagonal AC of length 6 cm. Measure ∠ ABC. Find the point R on AD such that RB = RC. Measure the length of AR.
Construct a ti.PQR, in which PQ=S. 5 cm, QR=3. 2 cm and PR=4.8 cm. Draw the locus of a point which moves so that it is always 2.5 cm from Q.
In Δ PQR, s is a point on PR such that ∠ PQS = ∠ RQS . Prove thats is equidistant from PQ and QR.
Draw and describe the lorus in the following cases:
The locus of points at a distance of 4 cm from a fixed line.
Describe completely the locus of points in the following cases:
Centre of a circle of varying radius and touching the two arms of ∠ ABC.
Construct a Δ ABC, with AB = 6 cm, AC = BC = 9 cm; find a point 4 cm from A and equidistant from B and C.
Using a ruler and compass only:
(i) Construct a triangle ABC with BC = 6 cm, ∠ABC = 120° and AB = 3.5 cm.
(ii) In the above figure, draw a circle with BC as diameter. Find a point 'P' on the circumference of the circle which is equidistant from Ab and BC.
Measure ∠BCP.
