Advertisements
Advertisements
प्रश्न
In Δ PQR, s is a point on PR such that ∠ PQS = ∠ RQS . Prove thats is equidistant from PQ and QR.
उत्तर
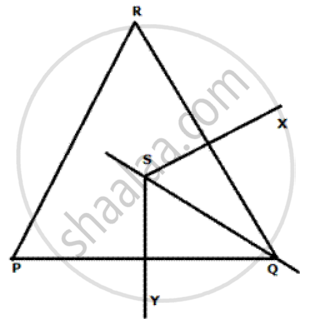
Steps of Construction:
(i) Draw line segment PQ.
(ii) With P and Q as centre draw intersecting arcs at R.
(iii) Join PR and RQ.
(iv) Draw angle bisector of angle Q.
(v) Draw perpendicular bisectors of PQ and RQ which meet the angle bisector at S. S is the required point.
(vi) In Δ QSY and Δ QSX
SQ= SQ
∠ SQY = ∠ SQX
∠ SYQ = ∠ SXQ = 90 degrees.
Therefore, Δ QSY and Δ QSX are congruent.
Hence, SY = SX and therefore S is equidistant from PQ and RQ.
APPEARS IN
संबंधित प्रश्न
On a graph paper, draw the line x = 6. Now, on the same graph paper, draw the locus of the point which moves in such a way that its distantce from the given line is always equal to 3 units
Construct a triangle ABC, with AB = 5.6 cm, AC = BC = 9.2 cm. Find the points equidistant from AB and AC; and also 2 cm from BC. Measure the distance between the two points obtained.
Ruler and compasses may be used in this question. All construction lines and arcs must be clearly shown and be of sufficient length and clarity to permit assessment.
- Construct a ΔABC, in which BC = 6 cm, AB = 9 cm and angle ABC = 60°.
- Construct the locus of all points inside triangle ABC, which are equidistant from B and C.
- Construct the locus of the vertices of the triangles with BC as base and which are equal in area to triangle ABC.
- Mark the point Q, in your construction, which would make ΔQBC equal in area to ΔABC, and isosceles.
- Measure and record the length of CQ.
Draw a straight line AB of 9 cm. Draw the locus of all points which are equidistant from A and B. Prove your statement.
Draw two intersecting lines to include an angle of 30°. Use ruler and compasses to locate points which are equidistant from these Iines and also 2 cm away from their point of intersection. How many such points exist?
Construct a rhombus ABCD whose diagonals AC and BD are 8 cm and 6 cm respectively. Find by construction a point P equidistant from AB and AD and also from C and D.
Construct a ti.PQR, in which PQ=S. 5 cm, QR=3. 2 cm and PR=4.8 cm. Draw the locus of a point which moves so that it is always 2.5 cm from Q.
In given figure 1 ABCD is an arrowhead. AB = AD and BC = CD. Prove th at AC produced bisects BD at right angles at the point M

Describe completely the locus of points in the following cases:
Centre of a circle of varying radius and touching the two arms of ∠ ABC.
Use ruler and compass only for the following question. All construction lines and arcs must be clearly shown.
- Construct a ΔABC in which BC = 6.5 cm, ∠ABC = 60°, AB = 5 cm.
- Construct the locus of points at a distance of 3.5 cm from A.
- Construct the locus of points equidistant from AC and BC.
- Mark 2 points X and Y which are at a distance of 3.5 cm from A and also equidistant from AC and BC. Measure XY.
